Какое-то время назад я разработал функцию, позволяющую строить прогнозы с использованием модели Комплексного экспоненциального сглаживания (Complex Exponential Smoothing — CES). Эта функция опубликована на сайте github под лицензией GPL v.3. С помощью этой функции можно давать прогнозы на произвольные промежутки времени как для не сезонных, так и для сезонных временных рядов. Кроме того, функция позволяет включать в модель экзогенные переменные. Давайте рассмотрим пример того, как она работает.

Для того, чтобы установить эту функцию себе на компьютер нужно установить пакет smooth из CRAN:

install.packages("smooth")

В качестве альтернативы можно установить пакет из GitHub. Для этого:

1.  Установить пакет «devtools», если он не установлен:

if (!require("devtools")){install.packages("devtools")}

2. Установить пакет «CES» с сайта github:

devtools::install_github("config-i1/smooth")

После того, как пакет установился, подключаем его в R:

library("CES")

Возьмём для наших примеров временной ряд №387 из базы рядов M3. Для того, чтобы база рядов была доступна, в R надо установить и подключить пакет «Mcomp»:

install.packages("Mcomp")
library("Mcomp")

Построим график по ряду:

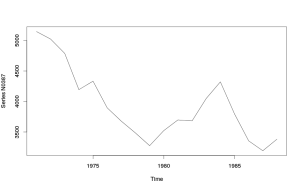
plot(M3$N0387$x,ylab="Series N0387")

Вот он:

Этот ряд относится к годовым, для таких рядов в M3 строят прогнозы на срок в 6 лет. Построим CES и дадим точечный и интервальный прогнозы. Делается это с помощью следующей команды:

ces(M3$N0387$x,h=6,intervals=T) -> test

Функция выдаёт много информации и возвращает кучу векторов и матриц. Поэтому мы используем «-> test» для сохранения этих данных в отдельный объект. Кроме того, она возвращает нам следующую информацию:

"Time elapsed: 0.19 seconds"
"Model constructed: Complex Exponential Smoothing"
"a0 + ia1: 1.88365413369954+0.97087980257933i"
"ABS Eigenvalues for stability condition:"
0.9364115 0.1399830
"CF value is: 1574102"
"AIC: 264.846; AICc: 267.922; BIC: 268.407; CIC:260.846"

Разберём по пунктам, что мы тут получили.

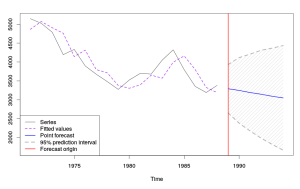
[1] — нам сообщают, что на построение модели ушло 0,19 секунд, что хорошо. Иногда, когда наблюдений много (например, 100), построение функции может затянуться на десятки секунд. Вызвано это тем, что R достаточно медленная программа. Возможно, я как-нибудь займусь C++ и перепишу код функции, тогда она будет работать значительно эффективней и быстрей. Но это планы на будущее. Сразу же стоит заметить, что скорость вычислений будет меняться от компьютера к компьютеру. Чем мощнее ваш железный конь, тем быстрее будут найдены оптимальные параметры модели.

[2] — нам сообщили, что построили модель Комплексного экспоненциального сглаживания. Альтернативы — та же модель, только с сезонностью.

[3] — мы видим значение комплексной постоянной сглаживания. По ней самой можно сказать, что CES даст прогноз на снижение (так как мнимая часть меньше единицы) и что ряд данных испытывает значительные изменения (так как действительная часть близка к 2).

[4] и [5] — далее нам выдали значения собственных чисел матрицы дисконтирования. Если все они меньше единицы, то полученная модель стабильна (то есть старые значения не влияют на прогноз). Если бы модель получилась нестабильной, нам бы об этом сообщили.

[6] — после этого мы видим значение целевой функции (сумма квадратов ошибок), которое само по себе полезной информации несёт немного.

[7] — и последнее — значения информационных критериев. Помимо трёх первых стандартных тут ещё рассчитывается комплексный информационный критерий (Complex IC — CIC), который представляет собой AIC с другим числом степеней свободы (см. соответствующую заметку).

Функция «ces» так же строит такой график:

Чтобы использовать прогноз CES, нам достаточно запросить его у R. Точечный прогноз:

test$forecast

Интервальный прогноз:

test$high
test$low

Если же нас интересует, насколько точно модель дала прогноз, мы можем включить тестовую выборку и немного изменить исходный запрос на:

x <- ts(c(M3$N0387$x,M3$N0387$xx),frequency=frequency(M3$N0387$x),start=start(M3$N0387$x))
ces(x,h=6,intervals=T,holdout=T) -> test

Первой строчкой мы объединили обучающую (M3$N0387$x) и тестовую (M3$N0387$xx) выборки в одну и сохранили это всё как объект «x» имеющий тип «ts» — временной ряд.

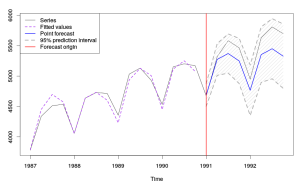
Второй строкой мы построили модель CES по обучающей выборке и дали прогноз на тестовую: команда holdout=T сообщает о том, что из всего ряда нужно h=6 последних наблюдений использовать для тестовой выборки. В результате использования этой команды мы получим немного другой вывод в командную строку:

"Time elapsed: 0.17 seconds"
"Model constructed: Complex Exponential Smoothing"
"a0 + ia1: 1.88365413369954+0.97087980257933i"
"ABS Eigenvalues for stability condition:"
0.9364115 0.1399830
"CF value is: 1574102"
"AIC: 264.846; AICc: 267.922; BIC: 268.407; CIC:260.846"
"MASE: 0.614"
"MASE.lvl: 5.224%"

Как видим, значения [1] — [7] идентичны предыдущему выводу, однако к ним добавились [8], сообщающий нам значение MASE для прогноза и [9] сообщающий нечто похожее только с делением на среднюю величину по исходному ряду данных. Эти значения сами по себе нам ни о чём не говорят, но позволяют сравнивать точность прогнозов разных моделей. MASE здесь используется, так как это наиболее адекватная и наименее смещённая мера точности прогноза. MASE.lvl так же является несмещённой, но при этом имеет некую интерпретацию, аналогичную обычной средней абсолютной процентной ошибки аппроксимации (MAPE).

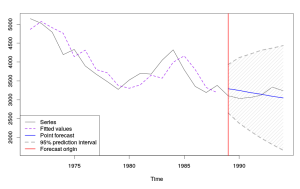
График всего это выглядит следующим образом:

Как видим, прогноз оказался достаточно точным. Впрочем, для какого-то однозначного вывода нужно его сравнить с прогнозами по другим моделям, чего в рамках это статьи мы пока делать не будем.

CES так же умеет строить прогнозы по сезонным временным рядам. Для этого ей нужно передать вектор типа «ts» и задать тип сезонной модели. Например, для сезонного ряда N2568 из M3 команда будет иметь следующий вид:

ces(M3$N2568$x,h=18,seasonality="F",intervals=T) -> test

Выбранная сезонность здесь — «полная» или «комплексная». Она позволяет моделировать как аддитивную, так  мультипликативную сезонность во временных рядах. В коде так же реализованы частичная («P»), она же просто аддитивная, сезонность и простая сезонная модель «S», не имеющая тренда. Подробней обо всём это можно будет почитать в скором времени в статье, которая готовится к выпуску.

А вот вывод нашей команды:

Non-stable model estimated! Use with care! To avoid that reestimate ces using 'bounds=TRUE'.
"Time elapsed: 4.34 seconds"
"Model constructed: Complex Exponential Smoothing with a full (complex) seasonality"
"a0 + ia1: 1.13652538578959+1.00295810649073i"
"b0 + ib1: 1.66249591228014+1.02106035157178i"
"ABS Eigenvalues for stability condition:"
1.0043258 0.6192850 0.1573755 0.1164405
"CF value is: 36299094"
"AIC: 2079.247; AICc: 2101.13; BIC: 2161.855; CIC:2047.247"

Как видим, R сообщил нам, что построена нестабильная модель (красная строка). Он нам так же предложил переоценить модель с параметром «bounds=TRUE», который отвечает за подбор параметров исключительно в области стабильных параметров. Это имеет смысл сделать, так как в противном случае прогноз может быть неадекватным и непредсказуемым (как бы это забавно не звучало), однако скорость вычислений в таком случае снизится.

Из нового в данном выводе — название модели (с полной сезонностью) и значение сезонной комплексной постоянной сглаживания [5]. Всё остальное аналогично предыдущему примеру. Заметим, что одно из собственных чисел в строке [7] оказалось больше единицы, что как раз и привело к жуткой красной надписи.

Перезапустим функцию с предложенным параметром:

ces(M3$N2568$x,h=18,seasonality="F",intervals=T,bounds=T) -> test

Итоговый вывод и прогноз изменятся:

"Time elapsed: 36.72 seconds"
"Model constructed: Complex Exponential Smoothing with a full (complex) seasonality"
"a0 + ia1: 1.14042311450241+0.99312271083681i"
"b0 + ib1: 1.62771138458957+1.04585709733533i"
"ABS Eigenvalues for stability condition:"
0.9999924 0.5183545 0.2109118 0.1898389
"CF value is: 36209112"
"AIC: 2078.959; AICc: 2100.842; BIC: 2161.567; CIC:2046.959"

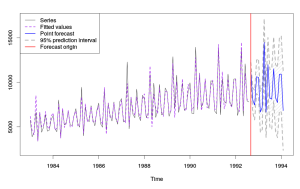
Время на вычисления теперь заняло 36,72 секунды, что почти в 10 раз больше, чем в предыдущий раз. Однако это привело к получению стабильной модели и нахождению коэффициентов, которые гарантируют немного меньшее значение целевой функции. Прогноз по CES в этом случае выглядит так:

Мы могли бы так же поиграться с тестовой выборкой, но делать этого не будем. Попробуйте проделать это сами ;).

Функция «ces» так же позволяет включать экзогенные переменные. В этом случае нужно ей передать в параметре «xreg» либо вектор (обычный либо «ts»), соответствующей переменной, либо матрицу (или «data.frame»), длинна которой должна либо соответствовать обучающей выборке, либо соответствовать обучающей выборке + горизонту прогнозирования. В первом случае значения экзогенных переменных экстраполируются методом Naïve.

К сожалению, под рукой у меня нет рядов данных, для которых можно было бы использовать экзогенные переменные, так что демонстрацию этой функции оставим на будущее.

Ну, и последнее, что включено в пакет «CES» — это функция «ces.auto», которая автоматически выбирает подходящую модель из несезонной / сезонной в зависимости от выбранного ряда данных. Делается это на основе информационного критерия. По умолчанию используется CIC, хотя можно попросить функцию выбрать и другой критерий. Посмотрим, как работает функция для ряда N2568:

ces.auto(M3$N2568$x,h=18,intervals=T,bounds=T) -> test

Построения моделей занимает какое-то время, но в конце концов мы получаем следующий вывод:

"Estimating CES with seasonality = 'N'"
"Estimating CES with seasonality = 'F'"

"The best model is with seasonality = 'F'"
"AIC: 2078.959; AICc: 2100.842; BIC: 2161.567; CIC: 2046.959"

Информации выводится немного, всё основное содержится в объекте «test». Самое главное — это то, что модель точно определила, что перед ней сезонный ряд данных.

Попробуем использовать эту же функцию для какого-нибудь ряда с аддитивной сезонностью и включим модель частичной сезонности. Для примера рассмотрим ряд N1192. Это ряд квартальных данных, период упреждения прогноза в нём обычно берётся равным 8 наблюдений.

x <- ts(c(M3$N1192$x,M3$N1192$xx),frequency=frequency(M3$N1192$x),start=start(M3$N1192$x))
ces.auto(x,h=8,model.types=c("N","P","F"),holdout=T,bounds=T,intervals=T) -> test

Параметр «model.types» передаёт функции все названия типов CES, которые нужно проверить по ряду данных. В результате применения этой функции получаем:

"Estimating CES with seasonality = 'N'"
"Estimating CES with seasonality = 'P'"
"Estimating CES with seasonality = 'F'"

"The best model is with seasonality = 'P'"
"AIC: 204.001; AICc: 234.001; BIC: 210.954; CIC: 197.001"
"MASE: 0.721"
"MASE.lvl: 3.885%"

Наилучшая модель — это модель с частичной сезонностью, так как ряд данных имеет аддитивную сезонную компоненту. Выглядит прогноз следующим образом:

Чисто графически видно, что точечный прогноз оказался недостаточно точным. Вызвано это малым количеством данных — точность CES повышается с ростом числа наблюдений. Тем не менее будущие значения попали в прогнозный интервал, так что не всё потеряно.

Применение той же команды для какого-нибудь другого ряда, только без сезонности, приводит к выбору несезонной модели CES. Можете поверить на слово, а можете сами проверить. Например, на ряде N1041.

По CES пока всё. Как только что-нибудь появится новое, обязательно напишу.

До новых встреч!