Смешенные модели экспоненциального сглаживания

В прошлых статьях мы обсудили чистые аддитивные и мультипликативные модели экспоненциального сглаживания. Логичным продолжением было бы обсуждение смешанных моделей, в которых некоторые компоненты имеют аддитивный характер, в то время как другие — мультипликативный. Однако я не хочу тратить на таких моделях много времени и решил упомянуть о них лишь вскользь. А всё потому, что я считаю, что такие модели не имеют особого смысла. Дело в том, что они противоречат логике моделирования. Ну, возьмём вот, например, какой-нибудь метод экспоненциального сглаживания Хольта-Уинтерса. Он соответствует статистической модели обозначаемой как ETS(A,A,M), в которой ошибка и тренд имеют аддитивный характер, а сезонность мультипликативная. Казалось бы, ничто не предвещает беды. Модель как модель. Однако первые две компоненты подразумевают, что ряд данных может иметь как положительные, так и отрицательные значения (ошибка так вообще считается распределённой нормально), а вот сезонность будет работать только, если мы имеем дело с положительными значениями. Если в ряде данных по какой-то причине будет отрицательное значение или, не дай бог, ноль, то быть беде! Это противоречие в рамках такой модели не разрешимо и является следствием смешения компонент.

Несмотря на это, некоторые смешанные модели работают вполне себе хорошо, когда мы имеем дело с положительными значениями и высоким уровнем ряда. Но не дай бог вам применить такую модель к ряду данных, в которых значения уменьшаются во времени. Например, прогнозировать продажи умирающего товара я бы с помощью таких моделей не стал, так как можно столкнуться с очень странным поведением и совершенно неадекватными прогнозами.

На этом краткое упоминание смешанных моделей можно считать законченным. Перейдём к более интересным вопросам.

Немного теории о выборе моделей и комбинировании

Теперь, когда мы так или иначе обсудили все возможные типы моделей экспоненциального сглаживания, время перейти к вопросу о том, как же выбрать из них наиболее подходящую. Фотиос Петропулос и Никос Курентзес показали в своём исследовании, что люди способны выбирать наилучшую модель вручную на основе визуального анализа временного ряда. Однако такой метод выбора моделей не всегда приемлем. Компаниям иногда бывает нужно, например, быстро получить прогнозы продаж своей продукции по всем магазинам страны. Это означает, что нужно выбрать наилучшую модель для каждого ряда из огромного массива данных (10000 рядов, например). Делать это вручную каждый раз, когда нужно получить прогноз — сродни сумасшествию. Именно поэтому существуют методы, позволяющие автоматизировать выбор моделей для прогнозирования.

Один из таких методов основан на информационных критериях. Именно он и реализован в функции es(). Роб Хайндман и компания показали в 2002 году, что этот метод работает достаточно хорошо. В 2006 году Бэкки Билла и др. показали, что метод работает одинаково хорошо с использованием разных информационных критериев. Функция es() позволяет осуществлять выбор с помощью AIC, AICc или BIC. Подробней на каждом из критериев мы тут останавливаться не будем, так как они уже были рассмотрены в электронном учебнике. Напомню лишь, что для того, чтобы выбрать наилучшую модель, нужно вначале построить все модели, которые хочется, затем рассчитать информационный критерий для каждой из них, после чего — выбрать ту, у которой критерий имеет наименьшее значение. В природе существует 30 моделей экспоненциального сглаживания, поэтому оценить все 30 из них — это непростая задача, требующая время. Чтобы ускорить этот процесс, я разработал алгоритм, с помощью которого можно из пула моделей выкинуть те, которые к данному временному ряду подходят заведомо плохо. Рассмотрим этот алгоритм подробней.

1. Оценивается модель ETS(A,N,N).
2. Оценивается модель ETS(A,N,A).
• Если информационный критерий модели (2) ниже критерия модели (1), значит в ряде данных есть какая-то сезонность. Это значит, что несезонные модели можно исключить, а пул моделей уменьшить с 30 до 20. После этого мы переходим к шагу (3).
• В противном случае в ряде данных нет сезонности, все сезонные модели можно убрать из рассмотрения, сократив таким образом пул моделей с 30 до 10. После этого мы переходим к шагу (4) алгоритма.

Эти два шага требуют небольшого пояснения. На данном этапе мы не оцениваем наличие тренда в ряде данных, так как ETS(A,N,N) является вполне неплохим аппроксиматором тренда. Безусловно прогноз по такой модели будет некорректным и неточным, но нас это пока не интересует, ряд она будет описывать хорошо. Постоянная сглаживания в этом случае будет близка к единице (а оптимальная и вовсе может быть больше), но это неважно, так как нас интересует на данном шаге определение сезонности. Если ряд сезонный (какой бы ни была сезонность: аддитивной или мультипликативной), то модель ETS(A,N,A) аппроксимирует его лучше, чем ETS(A,N,N). А значит и информационный критерий у неё будет ниже.

3. Оценивается модель ETS(A,N,M) и сравнивается с предыдущей.
• Если информационный критерий модели (3) ниже критерия модели (2), значит сезонность носит мультипликативный характер. Это сокращает пул моделей с 20 до 10. Можно переходить к шагу (4).
• Иначе сезонность можно считать аддитивной. Это также приводит к сокращению пула моделей с 20 до 10. После этого с чистой совестью можно переходить к шагу (4).
4. Оценивается модель с аддитивным трендом и либо без сезонности, либо с аддитивной или мультипликативной, в зависимости от результатов на шагах (2) и (3). Модель может быть соответственно: ETS(A,A,N), ETS(A,A,A) или ETS(A,A,M).
• Если информационный критерий на этом шаге ниже критерия на предыдущем, то в ряде данных есть тренд, значит пул моделей сокращается до восьми.
• В противоположном случае жизнь становится ещё проще, так как можно сказать, что тренда в данных нет, а значит нужно проверить всего одну модель — с мультипликативной ошибкой. Например, если мы до этого выяснили, что модель ETS(A,N,M) подходит к ряду данных лучше остальных, то нам остаётся только проверить модель ETS(M,N,M).

Аддитивный тренд на последнем шаге можно считать хорошей аппроксимацией всех остальных типов трендов. Если такая модель лучше модели без тренда, то далее можно попробовать определить тип тренда.

Описанный выше алгоритм позволяет вместо того, чтобы оценивать все 30 моделей, оценить только 4 или 12 из них (в зависимости от того, есть ли в ряде данных тренд или нет). Мои эксперименты показывают, что в большинстве случаев этот алгоритм гарантирует, что у полученной модели будет наименьшее значение информационного критерия. Впрочем, это не означает, что полученная модель будет давать самые точные прогнозы. Из-за разных случайных неучтённых факторов мы могли выбрать не ту модель. Для того, чтобы как-то учесть этот возможный провал, можно вместо того, чтобы выбирать только одну, скомбинировать несколько. Впрочем, нам сами модели менее интересны, чем прогнозы, которые они дают, так что будем комбинировать прогнозы. Тем более, что литература по прогнозированию говорит нам о том, что комбинированный прогноз оказывается в среднем точнее индивидуальных прогнозов моделей.

Очевидно, что вариантов комбинирования существует несчётное множество. Одно дело выбрать модели, чьи прогнозы скомбинировать, совсем другое — распределить веса между ними. Понятно, что веса надо распределять как-то неравномерно, а то модель ETS(A,N,N) будет иметь такой же вес, как и модель ETS(A,N,A) на сезонных данных, а это будет приводить к заведомо плохим результатам. Один из методов распределения весов, показавший свою эффективность — это метод на основе информационных критериев, рассмотренный в книге Burnham and Anderson. В соответствии с этим методом, веса для каждой из моделей в пуле рассчитываются по формуле:

\begin{equation} \label{eq:statLikelihoodAICweights}
w_j = \frac{ \exp \left(-\frac{1}{2} \left(\text{IC}_j -\min(\text{IC}) \right) \right)}{\sum_{i=1}^m \exp \left(-\frac{1}{2} \left(\text{IC}_i -\min(\text{IC}) \right) \right)},
\end{equation}
где \(m\) — это число моделей в пуле, IC\(_j\) — значение информационного критерия для модели номер \(j\), а \(\min(\text{IC})\) — это минимальное значение информационного критерия среди моделей в пуле. Модели с меньшими информационными критериями будут иметь больший вес, чем модели с большими значениями. Причём любой информационный критериq может быть использован вместо IC. К слову, Стефан Коласса показал, что при использовании этого метода комбинирования точность прогнозов ETS увеличивается. Этот метод реализован в функции es(). О том, как с ним работать в R, мы обсудим в следующем параграфе.

О том, как с этим работать в R

Ну что же, посмотрим, как это всё реализовано в функции es()? Начнём с простого.

Если мы не очень себе представляем, что делать с данными и надо ли как-то ограничивать пул моделей, то можно попросить функцию выбрать наилучшую из всех возможных 30 моделей. Это делается путём задания параметра model=»ZZZ». Точно так же включается выбор наилучшей модели в функции ets() пакета forecast (правда в ней происходит выбор из значительно меньшего числа моделей, из 16 вместо 30). В этом случае для выбора модели будет использован алгоритм описанные в предыдущем параграфе.

Например, для ряда N2568 из базы M3 у нас получится вот что:

es(M3$N2568$x, "ZZZ", h=18)

Это даст нам следующее:

Forming the pool of models based on... ANN, ANA, ANM, AAM, Estimation progress: 100%... Done! 
Time elapsed: 2.6 seconds
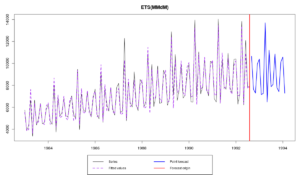
Model estimated: ETS(MMdM)
Persistence vector g:
alpha  beta gamma 
0.020 0.020 0.001 
Damping parameter: 0.965
Initial values were optimised.
19 parameters were estimated in the process
Residuals standard deviation: 0.065
Cost function type: MSE; Cost function value: 169626

Information criteria:
     AIC     AICc      BIC 
1763.990 1771.907 1816.309

Во время выбора модели функция будет сообщать нам, какие модели проверила: вначале это была ETS(A,N,N), затем — ETS(A,N,A), после неё — ETS(ANM) (это говорит о том, что в данных есть сезонность и функция пытается определить её тип), ну и, наконец, — ETS(A,A,M) (проверяется наличие тренда). Если нам всё это видеть ненужно, мы можем попросить функцию делать всё это про себя путём задания параметра silent=»all». Как видим, в результате этой процедуры наилучшей оказалась модель ETS(M,Md,M).

Заметим, что рассмотренный выше алгоритм выбора модели будет использован функцией только если хотя бы одна из компонент задана как «Z», а все остальные — как «Z», «A», «M» или «N». Если какие-то компоненты задать вручную («A», «M» или «N»), то процесс выбора пройдёт быстрее, так как пул моделей в этом случае уменьшится.

По умолчанию для выбора функция использует AICc, но пользователю так же доступны AIC и BIC:

es(M3$N2568$x, "ZZM", h=18, ic="BIC")

Что же, давайте теперь допустим, что по какой-то причине нас интересуют только аддитивные модели. Как нам выбрать наилучшую из них? Очень просто! Для этого используется значение «X» в компонентах. Например, таким вот образом мы проверим все возможные аддитивные модели экспоненциального сглаживания:

es(M3$N2568$x, "XXX", h=18)

В результате этого получим вот что:

Estimation progress: 100%... Done! 
Time elapsed: 0.72 seconds
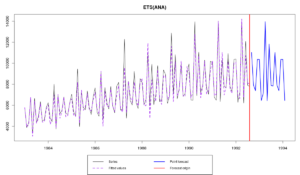
Model estimated: ETS(ANA)
Persistence vector g:
alpha gamma 
0.174 0.695 
Initial values were optimised.
16 parameters were estimated in the process
Residuals standard deviation: 609.711
Cost function type: MSE; Cost function value: 320472

Information criteria:
     AIC     AICc      BIC 
1831.789 1837.284 1875.847

В этом примере функция проверит подряд шесть моделей и выберет наилучшую из них. Пул чистых аддитивных моделей включает: ANN, AAN, AAdN, ANA, AAA и AAdA. Для этого ряда данных наилучшей оказалась ETS(A,N,A).

Похожим образом мы можем выбрать наилучшую модель из чистых мультипликативных. Для этого вместо «X» надо использовать «Y»:

es(M3$N2568$x, "YYY", h=18)

Функция так же проверит все шесть мультипликативных моделей и выберет наилучшую. В этот раз это будет ETS(M,Md,M). Модель YYY может быть особенно полезной в случае со значениями ряда, близкими к нулю.

Теперь, зная эти базовые черты, мы можем формировать произвольные пулы моделей, используя «X», «Y» и «Z». Например, мы можем составить такой пул моделей: MNN, MAN, MAdN, MNM, MAM, MAdM — используя команду:

es(M3$N2568$x, "YXY", h=18)

Получим вот что:

Estimation progress: 100%... Done!
Time elapsed: 0.92 seconds
Model estimated: ETS(MAdM)
Persistence vector g:
alpha  beta gamma 
0.021 0.021 0.001 
Damping parameter: 0.976
Initial values were optimised.
19 parameters were estimated in the process
Residuals standard deviation: 0.065
Cost function type: MSE; Cost function value: 169730

Information criteria:
     AIC     AICc      BIC 
1764.062 1771.979 1816.380

Если все пулы моделей, которые мы рассмотрели выше, нас не устраивают, и мы хотим сформировать какой-то свой собственный, особенный, то его можно передать функции в виде вектора названий:

es(M3$N2568$x, c("ANN", "MNN", "AAdN", "AAdM", "MAdM"), h=18)

В этом случае функция пройдёт через все модели в пуле и выберет наилучшую, которой в данном случае является ETS(M,Ad,M). Обратим внимание на то, что значение информационного критерия моделей ETS(M,Ad,M) и ETS(M,Md,M) очень близки друг к другу. Сразу же возникает вопрос, какой модели отдать предпочтение, если разница между ними настолько ничтожна. Именно такие вещи и мотивируют комбинирование прогнозов.

Комбинирование прогнозов регулируется в es() с помощью значения «C». Опять же, мы можем использовать «Z», «X», «Y», «N», «A» и «M» вместе с этим значением и комбинировать модели из тех пулов, которые нам нравятся. В простейшем же случае мы можем скомбинировать все 30 моделей вот так (давайте ещё попросим и интервал прогнозный построить):

es(M3$N2568$x, "CCC", h=18, intervals=TRUE)

Получим следующие результаты:

Estimation progress: 100%... Done!
Time elapsed: 10.04 seconds
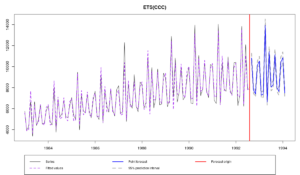
Model estimated: ETS(CCC)
Initial values were optimised.
Residuals standard deviation: 438.242
Cost function type: MSE

Information criteria:
Combined AICc 
     1772.198 
95% parametric prediction intervals were constructed

И вот такой график:

Из-за того, что мы задали «C» для всех компонент, функция прошла через все 30 моделей, что заняло около 10 секунд. Но мы могли бы скомбинировать и модели из меньшего пула, если бы знали, как его ограничить. Например, глядя на линейный график нашего ряда, можно заключить, что нам нужна модель с мультипликативной сезонностью:

es(M3$N2568$x, "CCM", h=18)

В этом случае мы скомбинируем 10 моделей, а значит и затратим раза в 3 меньше времени, чем в случае с комбинированием всего подряд.

Можно так же сформировать какой-нибудь экзотический пул на основе «X» и «Y»:

es(M3$N2568$x, "CXY", h=18)

В этом случае пул будет включать 12 моделей: ANN, AAN, AAdN, ANM, AAM, AAdM, MNN, MAN, MAdN, MNM, MAM, MAdM.

Ну, и наконец, мы можем скомбинировать модели из произвольного пула, если в него включить CCC:

es(M3$N2568$x, c("CCC","ANN", "MNN", "AAdN", "AAdM", "MMdM"), h=18)

Как видим, функция es() предоставляет огромный простор для творчества при выборе моделей и комбинировании прогнозов. Теперь вы можете творить с экспоненциальным сглаживанием всё, что захотите.

На сегодня всё. В следующий раз мы обсудим другие захватывающий параметры функции es(). Не переключайтесь!