Хотите уже наконец что-нибудь построить? Пока рановато. Для начала нужно проанализировать полученные данные. Это можно сделать используя графический и статистический анализ данных.
Графический анализ заключается в представлении данных в графическом виде и их последующему анализу. Самый простой из возможных и один из самых информативных графиков — это линейный график. Он позволяет посмотреть на изменение показателя во времени. Однако даже он может быть представлен по-разному.
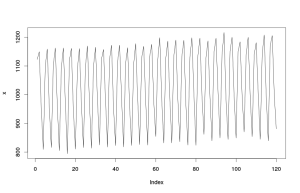
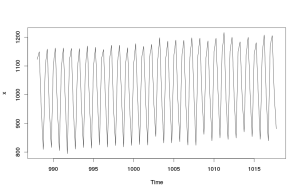
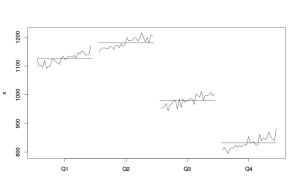
Если по оси абсцисс откладывать моменты времени, а по оси ординат — значения нашего показателя, то мы получим простой линейный график.
По этим построенным нами графикам видно, что изучаемый показатель растёт во времени и имеет чёткую квартальную сезонность. Явных выбросов в динамике нашего показателя не наблюдается, поэтому дополнительных исследований относительно причин происхождения необычных событий мы можем не проводить.
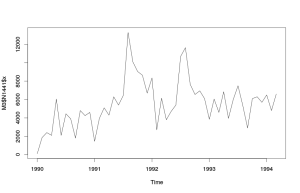
По этому графику видно, что показатель незначительно меняется во времени. При этом в середине 1991 и 1992 годов происходили какие-то события, выбивающиеся из общей динамики: значения оказывались выше 10000, при том, что в остальное время показатель не выходил за 8000. Для дальнейшего эффективного прогнозирования нам нужно попытаться выяснить причину такой аномалии. Что касается сезонности, то однозначное заключение о её наличии либо отсутствии сделать достаточно сложно. Ряд скорее носит случайный характер.
Как видим, уже простой анализ линейного графика нам даёт достаточно много информации.
Достаточно часто для эффективного прогнозирования нужно уметь определять сезонность. Если по первому ряду нам удалось её легко увидеть, то для однозначного вывода по второму ряду нам стоит построить дополнительные графики. Посмотрим на динамику показателя по отдельным годам.
Каждая линия на этом графике — это изменение показателя в пределах одного года. По такому графику видно, что каждый второй квартал наблюдается рост показателя (пик продаж), в то время как каждый четвёртый квартал значения оказываются ниже среднегодовых. Ряд обладает явной сезонностью.
Построив такой же график по ряду M3$N1441$x мы сезонности не увидим (проверьте сами).
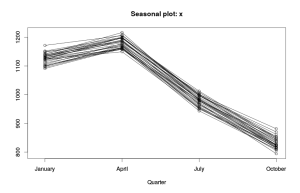
Похожий по смыслу но немного другой по представлению — график сезонной динамики. На нём показана динамика показателя по каждому из кварталов.
На графике показана динамика показательно отдельно по сезонам. Горизонтальными линиями на графике показаны средние значения по каждому из кварталов. Очевидно, что показатель демонстрирует рост из года в год, при этому сезонность носит достаточно явный характер.
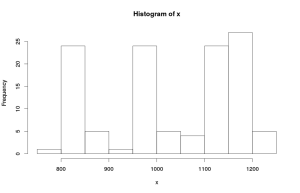
Другой взгляд на те же самые данные — это гистограмма. Она показывает, с какой частотой в ряде данных встречаются те или иные значения. Строится она достаточно просто — значения в ряде данных упорядочиваются по величине, исследователь задаёт интервалы и считает, сколько значений попало в эти интервалы.
По этому графику видно, что в исходном ряде данных имеются своеобразные подгруппы. Это читается по пикам в районе 800 — 850, 950 — 1000 и 1100 — 1200. В нашем случае мы знаем, чем это вызвано: всё той же сезонностью. Однако в других случаях может иметь смысл разобраться, что вызвало такое разделение ряда на части.
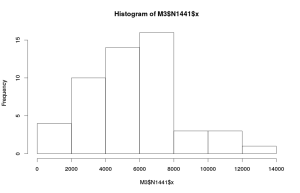
Для ряда 1441 получим следующую гистограмму:
По ряду 1441 видно, что большая часть значений лежит ниже 8000 — распределение этого показателя асимметрично. В этом случае значения выше 8000 могут быть связаны с какой-нибудь аномалией.
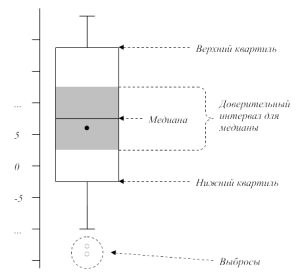
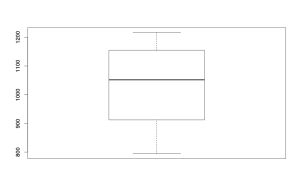
Немного другим представлением той же информации является ящичковая диаграмма (она же "boxplot" - "боксплот"). Она может быть представлена как вертикально, так и горизонтально ориентированной. На рисунке ниже показана ящичковая диаграмма с вертикальной ориентацией.
Дадим краткое пояснение каждому элементу на этой диаграмме.
Нижний и верхни квартили мы рассмотрели в параграфе про статистический анализ.
Расстояние между верхним и нижним квартилями называется интерквартильным расстоянием и обозначается IQR:
\( IQR = Q_3 - Q_1 \)
Медиану (\( Md(x) \)) мы так же обсудили в предыдущем параграфе.
Серой областью вокруг медианы выделен доверительный интервал, который рассчитывается с помощью формулы:
\( Md(x) \pm 1.57 \frac{ IQR } { \sqrt{T} } \),
где T — число наблюдений в выборке.
Иногда вместо тёмной области на ящичковой диаграмме изображают сужение к медиане. Там где это сужение начинается, находятся границы интервала.
Точкой в середине ящичковой диаграммы иногда обозначают среднюю величину по выборке. Если средняя величина лежит в пределах доверительного интервала медианы, то это косвенно указывает на то, что распределение изучаемой случайной величины симметрично.
Усы диаграммы ограничивают выборку сверху и снизу интервалами, рассчитываемыми на основе формул:
Нижний ус — \( Q_1 - 1.5 IQR \);
Верхний ус — \( Q_3 + 1.5 IQR \).
Если значения выходят за эти усы, то они считаются выбросами — величинами не вписывающимися в общую динамику.
Рассмотрим этот инструмент на нашем примере:
По первой ящичковой диаграмме сделать какие-либо интересные выводы затруднительно — распределение случайной величины там выглядит достаточно однородно. По расположению квартилей и медианы, однако, можно прийти к выводу об асимметрии в распределении.
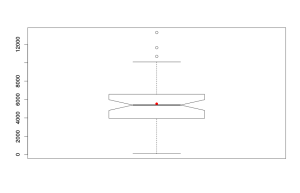
По ящичковой диаграмме по второму ряду видны выбросы (те самые значения больше 10000, на которые мы обратили внимание ранее) и заметно, что средняя величина оказалась незначительно выше медианы. Возможно, если учесть эти выбросы, распределение нашего показателя будет более симметричным, что в теории может облегчить процесс прогнозирования.
Построение гистограмм и ящичковых диаграмм обычно имеет больший смысл, когда оценивается качество полученной модели. В таком случае обычно анализируются ошибки (остатки) модели для того, чтобы выяснить, всё ли было взято в расчёт и нужно ли как-нибудь доработать модель.
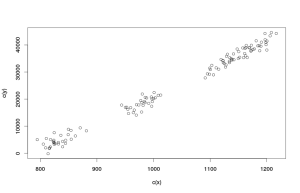
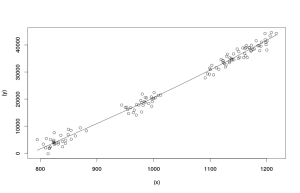
В случае если перед аналитиком стоит задача прогнозирования на основе нескольких переменных, имеет смысл изучить возможные связи между ними. В этом случае стоит обратиться к точечной диаграмме:
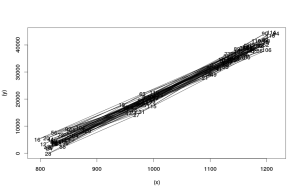
По полученной точечной диаграмме видно, что между нашими двумя переменными есть связь, близкая к линейной, выбросов либо явных изменений в связях не наблюдается. Это полезная информация, которая позволяет нам сделать вывод, что применение простой парной регрессии в данном случае может быть оправдано и оценки коэффициентов полученной модели не будут сильно искажёнными. Стоит заметить, что второй график (который мы тут назвали "Точечная диаграмма курильщика") имеет смысл строить только в тех случаях, когда исследователь подозревает, что в ряде данных могли произойти со временем изменения в связях. Просто так строить его не имеет никакого смысла, так как его крайне тяжело читать и интерпретировать.
Точечная диаграмма так же позволяет понять, имеем ли мы дело с однородной выборкой или же в наших данных имеются какие-то подгруппы. В нашем случае такие подгруппы имеются, но они все описываются одной и той же линейной зависимостью (все лежат на одной и той же линии).
В случае, если между двумя переменными имеется сложная нелинейная связь, бывает нелишним «сгладить» эти связи и проанализировать полученную зависимость.
По нему видно, что между нашими переменными имеется нелинейная зависимость (не удивительно, ведь мы же её и использовали при генерации переменной «y»). Впрочем, нелинейность в этом случае носит слабый характер и может быть проигнорирована.
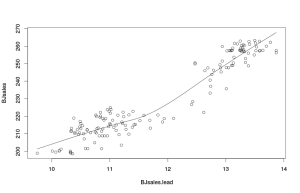
Более интересным представляется пример с рядами из пакета «datasets»:
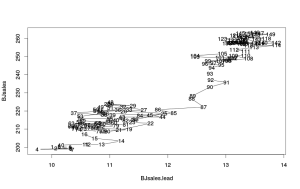
По этому графику уже видно, что значения независимой переменной до 12 влияют на продажи одним образом, но начиная примерно с 12 зависимость меняется (потому что меняется угол наклона прямой линии). Для того, чтобы понять, произошли ли эти изменения в связях со временем или же просто носят нелинейный характер (то есть наблюдается ли эволюция в связях), можно соединить точки на плоскости линиями следующим образом:
Главное, что видно по полученному графику - это то, что переход от одной группы к другой носит временной характер: до 86-го наблюдения зависимость имеет один вид, начиная примерно с 94-го - другой. Для эффективного прогнозирования такого ряд продаж возможно имеет смысл обратиться к моделям с меняющимся во времени параметрам, либо моделям оценённым методом неравномерного сглаживания. Если бы такого однозначного изменения во времени не наблюдалось, то можно было бы учесть эту нелинейность либо с помощью какой-нибудь математической функцией (например, с помощью полинома), либо с помощью фиктивных переменных.
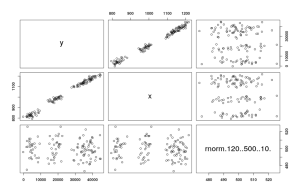
Если в распоряжении исследователя имеется множество переменных и ему требуется изучить возможны связи между переменными, то вместо того, чтобы строить вручную кучу точечных диаграмм можно построить матрицу точечных диаграмм.
Попробуем проанализировать полученный график. По матрице точечных диаграмм видно, что между «y» и переменной «x1» есть некоторая связь, близкая к линейной, но при этом никакой явной связи между «x1» и «x2», а так же между «y» и «x2» не наблюдается. Эта информация может позволить нам понять, стоит ли включать те или иные переменные в модель и как именно их включить.
Помимо рассмотренных нами тут графиков есть ещё различные столбиковые и круговые, но для целей прогнозирования они обычно несут мало информации.