Вот вы говорите: «Ну, что нам твоё прогнозирование?!». Ну, может, и не говорите, но точно подумали! Все эти странные формулы, общие слова об инерционности, какие-то квантильные регрессии, экспоненциальное сглаживание и прочее. Это же всё так далеко и оторвано от реальности, не так ли?
А вот и не так. И чтобы показать это, давайте-ка обсудим такую животрепещущую тему, как курс доллара. Правильней вообще-то было бы сказать «курс рубля», но пусть будет таки доллар. Он, вроде как, непосредственно нас не касается, но жутко портит жизнь тем, что лезет вверх (точнее рубль падает, но мы-то знаем, кто во всём виноват). Конечно, мы могли бы просто почитать какие-нибудь аналитические статьи, но мы же не ищем легких путей, не так ли? К тому же, намного интересней всё сделать самим, своими руками!
Но прежде чем начинать играться с модельками, обратимся к какой-нибудь приличной аналитике. Нам, ведь, для того, чтобы дать прогноз, нужно понять, что влияет на курс доллара. Один из достаточно адекватных обзоров, касающихся нашей темы, представлен в статье Андрея Мовчана, «Кризис в духе конца 80-х – возможный сценарий лет через пять». Достаточно важным в этой статье для нас является то, что автор обосновывает связь между курсом рубля и ценами на нефть — это то, на что ещё в своё время обратил внимание убитый в Москве Борис Немцов. Эта связь объясняется ресурсо-ориентированностью российской экономики и попыткой ЦБ отказаться от валютных интервенций (с целью укрепления рубля) с декабря 2014 года. То есть она может измениться в случае, если Россия перестанет опираться исключительно на импорт нефти и газа либо, если ЦБ вернётся к интервенциям. Но пока это не произошло, мы можем этим свойством пользоваться.
По-хорошему, для того, чтобы построить точную и адекватную прогнозную модель, нам нужно было бы учесть все факторы, влияющие на курс рубля: объём операций в валюте, объём иностранных инвестиций, бегство капитала, международные санкции, даже введённое Россией эмбарго на европейские продукты… — всё, что только может оказаться важным для объяснения динамики курса доллара. В этом случае мы могли бы построить прекрасную регрессионную модель с высокой объясняющей способностью. Однако нам нужно прогнозировать, а не объяснять, а для удовлетворения нашего любопытства достаточно и простой модели парной регрессии. К тому же, как это нам объяснил Спирос Макридакис, сложные модели не обязательно оказываются точнее простых. То есть мы можем добавить себе проблем, но это не будет гарантировать нам повышения в точности.
Итак, построим что-нибудь типа:
\begin{equation} \label{eq:generalreg}
\hat{y}_t = f(x_t) ,
\end{equation}
где \(y_t\) — это курс доллара, \(x_t\) — цена барреля нефти, \(f\) — некая функция, вид которой нам ещё предстоит определить.
В идеальных условиях мы должны были бы выбрать данные по ценам на нефть марки Urals (как раз то, что Россия и экспортирует), но у меня этих данных под рукой не оказалось, зато были данные по ценам марки Brent. Это дневные данные с начала 2010 года по 20 августа 2015-го, собранные из сети Интернет с помощью двух рук, клавиатуры, Linux и небольших интеллектуальных усилий. Данные же по курсу доллара легко берутся с сайта Центробанка. После удаления отсутствующих значений и преобразования рядов данных в объекты «xts» в R, было получено несколько объектов, которые я бережно сохранил в следующий файл специально для вас: файл с данными для R.
Для дальнейшей работы в R нам понадобятся пакеты xts и quantreg:
install.packages("xts")
install.packages("quantreg")
Первый пакет позволяет привязать каждое фактическое значение к конкретной дате, а второй позволяет строить квантильные регрессии, которые мы вскользь упоминали в параграфе «Простые методы оценки параметров моделей».
А теперь давайте-ка я поясню, что содержится в файле «usd.Rdata»:
- brent — это матрица с датами и ценами на нефть марки Brent,
- brent.xts — всё те же самые данные, но преобразованные в объект «xts»,
- usd — матрица с датами и курсами доллара по дням,
- usd.xts — то же самое, только в «xts»,
- brent.data — объединённые данные brent.xts и usd.xts после очищения,
- brent.data.used — часть предыдущего ряда (начиная с 1 июля 2014), упорядоченная по Brent.
Вначале посмотрим на ряды данных:
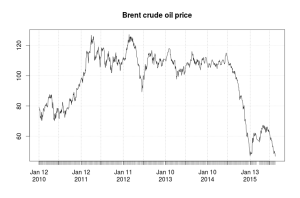
plot(brent.data$Brent,main="Brent crude oil price")
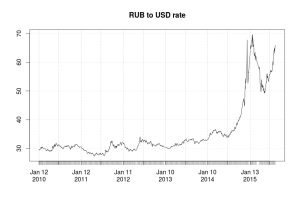
plot(brent.data$USD,main="RUB to USD rate")
Первый ряд говорит нам о том, что будущее не предсказуемо и о возвращении к 100 долларам за баррель нефти вполне можно помечтать, но явно не в краткосрочной перспективе.
По второму ряду видно, что рубль стабильно падает (а значит, курс доллара растёт), но до 2013-го года он это делал очень медленно, периодически прибавляя в цене, а вот, начиная с 2013-го года, наметилась более уверенная тенденция к росту курса доллара, которая затем в 2014-м усилилась. Как указывают во всяких русофобских статьях на непатриотичных сайтах, это было вызвано снижением инвестиций в Россию и бегством капитала из-за ухудшения политической ситуации. Но, скорее всего, всё это не так, во всём просто виноваты пиндосы.
Сопоставляя эти два графика, можно заметить, что та самая пресловутая зависимость между показателями появилась относительно недавно — приблизительно с начала июля 2014 года. Впрочем, давайте взглянем на точечную диаграмму по показателям. Вначале за весь период (с 2010-го года):
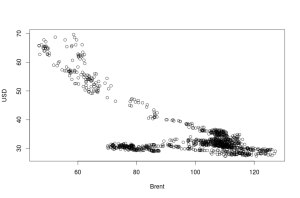
plot(as.matrix(brent.data))
По этому графику тоже видно, что длительное время чёткой зависимости не наблюдалось (чёрное облако внизу), но затем что-то изменилось и связь появилась. Поэтому для эффективного прогнозирования нам нужно оставить только нужный кусок данных, а от старых избавиться — иначе они будут вносить серьёзные искажения в прогнозную модель. Чисто визуально, по предыдущим двум графикам, видно, что тенденция к снижению цен на нефть началась с начала июля, в это же время и начался рост курса доллара. Поэтому для дальнейшего анализа возьмём данные с 1 июля 2014. По идеи, эту дату надо было бы как-то обосновать, объяснить каким-нибудь важным историческим событием, но мне этого делать совершенно не охота. Впрочем, знаю. 1 июля 2014-го года в России вступил в силу закон о запрете мата в кино, литературе и на сцене. Вот он во всём и виноват!
Итак, точечная диаграмма по этим усечённым данным выглядит так:
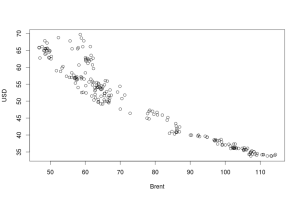
plot(brent.data.used)
По этому графику видно, что зависимость носит нелинейный характер: с ростом цен на нефть, курс рубля укрепляется (курс доллара падает), но при этом по мере увеличения цены на нефть рубль укрепляется всё медленней. Зависимостям этого типа соответствуют такие математические функции, как экспонента и гипербола. У гиперболы есть одно более реалистичное свойство — при приближении \(x\) к нулю, \(y\) стремится к бесконечности. Действительно, если бы цена на нефть приближалась к нулю (бред, но всё же), то Российская экономика была бы в жутком кризисе, а рубль превратился бы в труху. Экспонента при всём этом допускает наличие не только нулевых, но и отрицательных цен на нефть…
Итак, гипербола! Построим для начала в R простую линейную регрессию:
lmmodel <- lm(USD~I(1/Brent),data=brent.data.used)
lm - это функция в R, которая позволяет строить линейные модели регрессий, I - это функция, позволяющая интерпретировать 1 / Brent, как единый регрессор.
Если теперь вызвать объект lmmodel, то получится примерно такой вывод:
Call:
lm(formula = USD ~ I(1/Brent), data = brent.data.used)
Coefficients:
(Intercept) I(1/Brent)
9.58 2815.11
О чём это всё нам говорит? На самом деле, не о многом. Просто о том, что построена регрессионная модель вида:
\begin{equation} \label{eq:lmreg}
\hat{y}_t = 9.58 + 2815.11 \cdot \frac{1}{x_t} ,
\end{equation}
Ещё мы знаем, что для каждого конкретного \(x_t\) значение прогнозируемого \(y_t\) будет соответствовать некой средней величине (т.н. условной средней). Что-то пытаться интерпретировать в этой модели не очень интересно, да и не совсем продуктивно. Лучше попробуем прикинуть, что произойдёт, если, например, цена нефти упадёт до 40 долларов за баррель. Подставим \(x_t = 40\):
\begin{equation} \label{eq:lmregfor}
\hat{y}_t = 9.58 + 2815.11 \cdot \frac{1}{40} \approx 79.96,
\end{equation}
Полученное значение указывает на то, что в среднем при такой цене на нефть курс доллара будет составлять примерно 79,96 руб/$. Но будущее в принципе неизвестно, поэтому в реальности может получиться и что-то выше / ниже.
В R получить этот же ответ легко с помощью команды:
coef(lmmodel) %*% c(1, 1/40),
где coef - это вектор коэффициентов, %*% - это символ матричного перемножения, а число 1 нужно для константы.
Однако ограничиваться одними лишь средними скучно, поэтому обратимся к квантилям. Для начала построим медианную регрессию с помощью функции rq() из пакета quantreg (не забудьте его загрузить: library("quantreg")).
medianmodel <- rq(USD~I(1/Brent),data=brent.data.used)
Получится вот что:
Call: rq(formula = USD ~ I(1/Brent), tau = 0.5, data = brent.data.used) Coefficients: (Intercept) I(1/Brent) 9.861377 2733.534440 Degrees of freedom: 218 total; 216 residual
Отличия в коэффициентах от предыдущей модели несущественны, но всё-таки есть. Эта модель уже даст нам значения, разделяющие выборку на две части: половина её будет ниже линии, а другая - выше. Например для той же цены в 40 долларов:
coef(medianmodel) %*% c(1, 1/40)
получим примерно 78.20 рублей за доллар. То есть в 50% случаев курс доллара будет ниже этой величины, а в других 50% - выше. Использование медианной модели можно обосновать тем, что курс, с которым мы имеем дело, явно имеет ненормальное распределение, возможно, какое-нибудь лог-нормальное. Средняя величина в этом случае будет давать завышенные значения, а вот медиана даст более точную оценку наиболее часто встречающихся значений.
Всё это прекрасно, но любое адекватное прогнозирование должно сопровождаться доверительными интервалами, иначе это просто тычок пальцем в небо. Так что построим-ка мы ещё две квантильные регрессии, соответствующие 2,5% и 97,5% квантилям (между ними будет лежать 95% всех наблюдений):
q025model <- rq(USD~I(1/Brent),data=brent.data.used,tau=0.025) q975model <- rq(USD~I(1/Brent),data=brent.data.used,tau=0.975)
Опустим вывод коэффициентов, посмотрим сразу на значения курса доллара:
coef(q025model) %*% c(1, 1/40) coef(q975model) %*% c(1, 1/40) > 72.01 > 102.40
А вот это уже более интересная информация. Эти цифры говорят нам о том, что в 95% случаев при цене на нефть в 40 долларов за баррель курс доллара будет лежать в пределах от 72 до 102 рублей за доллар. Причём, беря во внимание медиану, в 47,5% случаев (то есть с вероятностью 0,475) курс будет лежать в пределах от 72,01 до 78,20 рублей за доллар.
Если теперь все расчётные значения нанести на нашу точечную диаграмму:
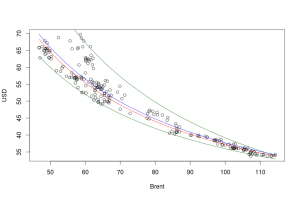
plot(brent.data.used) lines(as.matrix(brent.data.used$Brent),fitted(medianmodel),col="red") lines(as.matrix(brent.data.used$Brent),fitted(q025model),col="darkgreen") lines(as.matrix(brent.data.used$Brent),fitted(q975model),col="darkgreen") lines(as.matrix(brent.data.used$Brent),fitted(lmmodel),col="blue")
то получится следующий приятный график:
На нём показаны расчётные значения наших четырёх моделей. Заметно, что использование средней (синяя линия) и медианы (красная линия) описывает тенденцию в целом, но не даёт представлений о границах, то есть по ним не понятно, чего можно ожидать в, скажем так, плохой и хорошей ситуациях.
Ну, и напоследок попробуем использовать экстраполяционные методы в прогнозировании цен на нефть. Будем использовать всё тот же кусок ряда с 1 июля 2014 года и построим прогнозы по модели экспоненциального сглаживания с демпфированным трендом (она хорошо зарекомендовала себя на практике в ряде соревнований и испытаний) с помощью функции ets() пакета forecast:
library("forecast")
aadnmodel <- ets(as.vector(brent.xts[1267:1480]),model="AAN",damped=TRUE)
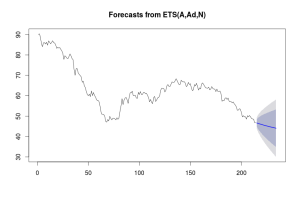
plot(forecast(aadnmodel,h=20))
Горизонт прогнозирования в 20 наблюдений примерно соответствует сроку в 1 месяц. Функция forecast позволяет сразу же построить и прогнозные интервалы, поэтому в итоге получится такой график:
Среднее значение на месяц вперёд по этой модели составляет около 44, верхняя граница 95% интервала - 58, нижняя - порядка 30. Подставим теперь эти значения в наши квантильные регрессии, чтобы получить условные прогнозы.
Оптимистичный вариант (58 долларов за баррель):
coef(q025model) %*% c(1, 1/58) coef(medianmodel) %*% c(1, 1/58) coef(q975model) %*% c(1, 1/58) > 53.37 > 56.99 > 69.71
Средний вариант (44 долларов за баррель):
coef(q025model) %*% c(1, 1/44) coef(medianmodel) %*% c(1, 1/44) coef(q975model) %*% c(1, 1/44) > 66.55 > 71.99 > 92.82
Пессимистичный вариант (30 долларов за баррель):
coef(q025model) %*% c(1, 1/30) coef(medianmodel) %*% c(1, 1/30) coef(q975model) %*% c(1, 1/30) > 92.04 > 100.98 > 137.51
Анализируя полученные данные, можно заключить, что в случае, если цена за баррель будет снижаться с замедлением (как нам спрогнозировала модель ETS(AAdN) - 44 доллара за баррель), то через месяц можно ожидать курс доллара в пределах примерно от 66 до 93, с медианной величиной в районе 72. При плохом стечении обстоятельств (30 долларов за баррель), курс может вполне дойти до 100 рублей за доллар (а то и до 138). При благоприятном стечении обстоятельств (58 долларов за баррель), курс вернётся до отметки 57 рублей за доллар (не забываем про доверительные интервалы).
В этом месте стоит посмотреть, что говорят аналитики.
Всё тот же Андрей Мовчан в своей статье упоминает себестоимость производства разных сортов нефти (похожую информацию можно найти и здесь). Он утверждает, что порядка 70% добываемой нефти имеет себестоимость в 45 долларов за баррель и ниже. Это означает, что при цене в 44 (наш средний прогноз), 30% нефти будет производиться в убыток. В краткосрочной перспективе это вполне возможно, но в долгосрочной, скорее всего, либо технологический процесс будет как-нибудь оптимизирован (что маловероятно), либо нерентабельные точки начнут прекращать добычу. Первое приведёт к остановке на уровне где-то ниже 45, второе приведёт к росту цены выше 45. В случае, если цена таки упадёт до 40, нерентабельными окажется уже порядка 50% предприятий. В общем, сценарий в 30 долларов за баррель в течение месяца возможен, но выглядит мало реалистичным.
Подводя итог всему этому, курс рубля скорее всего будет падать (а значит доллар будет расти). 70 рублей за доллар через месяц, при условии сохранения всех сложившихся тенденций, выглядит вполне ожидаемым. Курс в 90 - менее вероятным, ещё выше - практически нереальным. Но, конечно же, никто не отменял чёрных лебедей. Кто знает, может, наш президент решит вернуть на родину ещё какую-нибудь часть какой-нибудь страны?.. В общем, как оно там будет на самом деле - покажет время. Будущее всё-таки не предопределено.