Теперь, когда мы обсудили основные черты функции es(), мы можем перейти к тому, как оптимизационный механизм работает, как параметры ограничиваются и как задаются стартовые значения при оптимизации функции es(). Эта статья написана для тех исследователей, которым важно знать, как работает тёмная сторона es().

Заметим, что в этой статье, мы будем обсуждать стартовые значения параметров. Не перепутайте со стартовыми значениями компонент экспоненциального сглаживания. Последние — это всего лишь часть первого.

Что ж, начнём.

Перед запуском оптимизации, нам нужно каким-то образом задать стартовые значения параметров. Число параметров и тип инициализации зависит от выбранной модели. Рассмотрим, последовательно, как каждый из них задаётся.

Постоянные сглаживания \(\alpha\), \(\beta\) и \(\gamma\) (для уровня ряда, тренда и сезонности) для аддитивной модели задаются равными 0.3, 0.2 и 0.1 соответственно. В случае с мультипликативной моделью они равны 0.1, 0.05 и 0.01. В общем случае мы стараемся найти параметры близкие к нулю, так как они позволяют сгладить ряд. Впрочем, это не всегда удаётся сделать, иногда ряд имеет более реактивные компоненты. Что касается мультипликативных моделей, стартовые значения там должны быть достаточно близкими к нулю, иначе модель может стать излишне чувствительной к шуму.

Следующий важный параметр — это параметр демпфирования тренда \(\phi\). Его стартовое значение задаётся в функции равным 0.95. В случае, когда он равен единице, мы получаем модель обычного тренда, из которой оптимизатору может быть затруднительно выбраться. Если же задать его слишком маленьким, то тренд может оказаться «передемпфированным», в результате чего траектория будет напоминать простую прямую горизонтальную линию.

Стартовые значения вектора состояний задаются в зависимости от типа модели. Вначале задаются значения для уровня и тренда. Происходит это путём оценки параметров следующей простой регрессионной модели по первым 12 наблюдениям (ну, или по все выборке, если в нашем распоряжении меньше 12 наблюдений):
\begin{equation} \label{eq:simpleregressionAdditive}
y_t = a_0 + a_1 t + e_t .
\end{equation}

В случае с мультипликативным трендом модель имеет следующий вид:
\begin{equation} \label{eq:simpleregressionMulti}
\log(y_t) = a_0 + a_1 t + e_t .
\end{equation}

В обоих случаях константа \(a_0\) используется в качестве стартового значения для уровня, а угол наклона \(a_1\) используется для тренда. В ситуации с мультипликативной моделью параметры экспонируются. В случае, если компонента тренда в модели отсутствует, вместо \(a_0\) для уровня используется средняя по той же части ряда.

В случае с сезонной моделью, проводится классическая декомпозиция с помощью функции decompose(), в которой тип сезонности соответствует выбранному пользователем. В итоге полученные сезонные коэффициенты используются для стартовых значений сезонной компоненты.

Все значения затем собираются в один вектор под названием C (да, я знаю, что это плохое название для вектора параметров, но так уж тут повелось) в следующем порядке:

1. Вектор постоянных сглаживания \(\mathbf{g}\) (persistence);
2. Параметр демпфирования \(\phi\) (phi);
3. Стартовые значения не сезонной части вектора состояний \(\mathbf{v}_t\) (initial);
4. Стартовые значения сезонной части вектора состояний \(\mathbf{v}_t\) (initialSeason);

После этого в вектор добавляются параметры для экзогенных переменных, которые мы тут пока обсуждать пока не будем:

5. Вектор параметров экзогенных переменных \(\mathbf{a}_t\) (initialX);
6. Матрица переходов экзогенных переменных (transitionX);
7. Вектор постоянных сглаживания для экзогенных переменных (persistenceX).

Если пользователь задаст в функции какие-то из упомянутых выше параметров (например, параметр initial), то этот шаг в формировании вектора C будет пропущен.

Помимо этого при оптимизации задаются границы для каждого из параметров. Это делается посредством двух векторов: CLower и CUpper, длина которых соответствует длине C. Эти ограничения зависят от того, какие значения принимает параметр bounds в функции es() и позволяют ускорить процесс нахождения оптимальных значений. Большая часть элементов CLower и CUpper носят чисто технический характер и нужны для того, чтобы полученная модель имела смысл (например, чтобы мультипликативные компоненты не были отрицательными). Единственный параметр, которые стоит упомянуть — это параметр демпфирования \(\phi\). Область его значений — это от нуля до единицы (включая границы). В этом случае прогнозные траектории не будут иметь взрывной харакетер.

В то время как вектора CLower и CUpper ограничивают более широкую область значений для всех параметров, значения постоянных сглаживания должны регулироваться более филигранно, так как они обычно влияют друг на друга. Поэтому эта регуляция происходит в самой целевой функции.

Если пользователь выбрал bounds=»usual», то границы задаются следующим образом:
\begin{equation} \label{eq:boundsUsual}
\alpha \in [0, 1]; \beta \in [0, \alpha]; \gamma \in [0, 1-\alpha] \end{equation}

В этом случае экспоненциальное сглаживание сохраняет свойство средне-взвешенной модели: веса между наблюдениями распределяются так, что более новые наблюдения имеют больший вес, каждый вес лежит в пределах от нуля до единицы, а сумма весов оказывается равной единице.

В случае, если пользователь задаст bounds=»admissible» (расширенные границы), то ограничения выводятся на основе собственных чисел матрицы дисконтирования. Функция проверяет, все ли модули собственных чисел лежат в пределах от нуля до единицы. Это гарантирует то, что веса убывают экспоненциально и их сумма равна единице. Однако в этом случае каждый отдельный вес может выходить за рамки промежутка (0, 1). В этом случае модель теряет свойство усредняющей, но не теряет свой фундаментальный смысл.

В экстремальном случае пользователь может и вовсе отказаться от границ постоянных сглаживания, задав bounds=»none».

Если во время оптимизации постоянные сглаживания выходят за заданные границы, то целевая функция возвращает очень большое число (\(10^{300}\)),а оптимизатор пытается подобрать следующие значения для постоянных сглаживания.

Для того, чтобы оптимизировать модель экспоненциального сглаживания, я использую функцию nloptr() из пакета nloptr. Это функция нелинейной оптимизации, написанная в C. Функции пакета smooth используют два алгоритма: BOBYQA и Nelder-Mead. Это делается в два шага: на первом параметры оцениваются с помощью BOBYQA, полученные оптимизированные параметры используются далее на втором шаге и подтягиваются ближе к оптимальным значениям с помощью Nelder-Mead. В случае со смешанными моделями, после первого шага, мы так же проверяем, отличаются ли полученные параметры от заданных перед оптимизацией. Если нет, то это означает, что оптимизация не удалась и BOBYQA используется повторно, но уже с другими значениями вектора C (постоянные сглаживания, которые не удалось оптимизировать обнуляются). Если оптимизировать модель не удаётся, вы можете передать оптимизатору параметры, контролирующие максимальное число итераций (maxeval) и относительную величину схождения (xtol_rel). Из стандартные значения и общий смысл кратко рассмотрены в документации к функциям.

В целом, такой механизм оптимизации гарантирует, что параметры будут близки к оптимальным значениям, будут лежать в разумных пределах и соответствовать требованиям выбранной модели.
Рассмотрим несколько примеров использования функции es(). Возьмём для этого ряд N41 из базы M3.

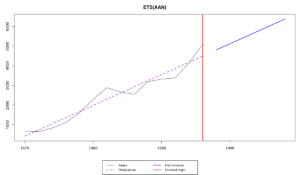
ETS(A,A,N) со стандартными границами в этом случае выглядит так:

es(M3$N0041$x,"AAN",bounds="u",h=6)

Time elapsed: 0.1 seconds
Model estimated: ETS(AAN)
Persistence vector g:
alpha  beta 
    0     0 
Initial values were optimised.
5 parameters were estimated in the process
Residuals standard deviation: 397.628
Cost function type: MSE; Cost function value: 101640.73

Information criteria:
     AIC     AICc      BIC 
211.1391 218.6391 214.3344

Как видим, обе постоянные сглаживания оказались равными нулю. Это означает, что мы совсем не используем новую поступающую информацию, а для прогноза используем лишь детерминистский тренд:

А вот, что произойдёт, если мы обратимся к расширенным границам:

es(M3$N0041$x,"AAN",bounds="a",h=6)

Time elapsed: 0.11 seconds
Model estimated: ETS(AAN)
Persistence vector g:
alpha  beta 
1.990 0.018 
Initial values were optimised.
5 parameters were estimated in the process
Residuals standard deviation: 327.758
Cost function type: MSE; Cost function value: 69059.107

Information criteria:
     AIC     AICc      BIC 
205.7283 213.2283 208.9236

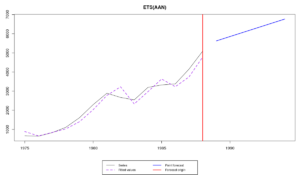
Как видим, постоянная сглаживания уровня ряда \(\alpha\) оказалась выше единицы. Она вообще почти равна двум. Это означает, что ETS потеряла свойство усредняющей модели. Тем не менее с такими значениями веса всё равно убывают во времени. Такое высокое значение параметра говорит о том, что уровень претерпевает существенные изменения. Это нестандартное поведение экспоненциального сглаживания и обычно не то, чего мы хотели бы получить от модели. Но такое случается.

А вот как это всё выглядит графически:

Хотелось бы заметить, что модель может быть стабильной даже в случае, если постоянные сглаживания оказались отрицательными. Так что не пугайтесь. И имейте в виду, что в случае нарушения свойства стабильности, функция вас об этом предупредит.

Помимо этого, пользователь может сам регулировать, какие стартовые значения использовать для векторов C, CLower и CUpper на первом шаге оптимизации. Выбор модели в этом случае невозможен, так как длина векторов в каждой модели будет разной. Пользователь так же должен удостовериться, что он передаёт вектора правильной длины (соответствующей выбранной модели). Эти значения можно передать с помощью … следующим образом:

Cvalues <- c(0.2, 0.1, M3$N0041$x[1], diff(M3$N0041$x)[1])
es(M3$N0041$x,"AAN",C=Cvalues,h=6,bounds="u")

Time elapsed: 0.1 seconds
Model estimated: ETS(AAN)
Persistence vector g:
alpha  beta 
    1     0 
Initial values were optimised.
5 parameters were estimated in the process
Residuals standard deviation: 429.923
Cost function type: MSE; Cost function value: 118821.938

Information criteria:
     AIC     AICc      BIC 
213.3256 220.8256 216.5209

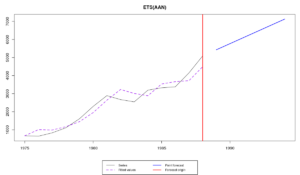
В этом случае мы получили граничные значения для обеих постоянных сглаживания. В результате этого получилась модель, в которой уровень имеет форму «случайного блуждания», а тренд не меняется во времени. Это несколько странное, но вполне возможное сочетание компонент. Аппроксимация и прогноз по модели оказываются похожими на то, что мы получили, когда использовали расширенные границы:

С помощью всего этого можно ненароком получить бессмысленную модель, так что будьте осторожны с тем, что задаёте и как. Например, следующие параметры приводят к тому, что в нашем распоряжении оказывается нечто невразумительное (с точки зрения прогнозирования):

Cvalues <- c(2.5, 1.1, M3$N0041$x[1], diff(M3$N0041$x)[1])
CLower <- c(1,1, 0, -Inf)
CUpper <- c(3,3, Inf, Inf)
es(M3$N0041$x,"AAN",C=Cvalues, CLower=CLower, CUpper=CUpper, bounds="none",h=6)

Time elapsed: 0.12 seconds
Model estimated: ETS(AAN)
Persistence vector g:
alpha  beta 
2.483 1.093 
Initial values were optimised.
5 parameters were estimated in the process
Residuals standard deviation: 193.328
Cost function type: MSE; Cost function value: 24027.222

Information criteria:
     AIC     AICc      BIC 
190.9475 198.4475 194.1428 
Warning message:
Model ETS(AAN) is unstable! Use a different value of 'bounds' parameter to address this issue!

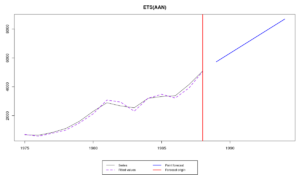
Несмотря на то, что такая модель лучше всех остальных аппроксимирует временной ряд (MSE оказалась равной 24027 против 70000 — 120000 в других моделях), она оказалась нестабильной, что означает, что старая информация имеет больший вес, чем новая. Прогноз в этом случае получился неразумным и, скорее всего, смещённым и неточным:

Так что будьте осторожны во время ручного задания параметров моделей.

Всем всех благ!