Вот мы проанализировали данные, вот мы сгладили временной ряд, выявили связи между переменными и решили построить некоторую математическую прогнозную модель. Давайте допустим, что мы пока решили ограничиться какой-нибудь простой моделью парной регрессии, например, такой вот:

\begin{equation} \label{eq:estim_linreg}
y_t = a + b x_t + e_t ,
\end{equation}

где \(y_t\) — объём продаж мороженого, \(x_t\) — температура воздуха, а \(e_t\) — случайная ошибка модели.

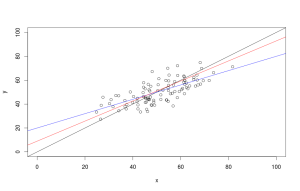
Вроде бы ничего особенного и ничего сложного, но откуда же нам взять коэффициенты \(a\) и \(b\)? Надо их как-то рассчитать (или, как это говорят в статистике, «оценить»). Для этого существует множество различных методов, но все они преследуют одну и ту же цель — оптимизировать какую-нибудь функцию (минимизировать или максимизировать) путём подбора этих самых значений \(a\) и \(b\). По сути вся задача сводится к тому, чтобы провести некоторым образом линию через «облако» значений \(x\) и \(y\) так, чтобы минимизировать целевую функцию. На рисунке ниже показан пример такого облака и нескольких линий, проходящих через него.

Мороженое и палочки

Каждая из линий на рисунке соответствует одной и той же линейной функции \eqref{eq:estim_linreg}, но с разными коэффициентами. Фактически любая такая линия — это последовательность некоторых расчётных значений \(\hat{y}_t\), позволяющая оценить, какими будут продажи мороженного в среднем если температура будет принимать значения \(x_t\) (отложенные по оси абсцисс). Очевидно, что таких прямых на плоскости можно провести сколько угодно, и каждая из них будет минимизировать либо максимизировать какой-нибудь свой критерий. Обычно это происходит путём подбора коэффициентов с использованием различных оптимизационных методов, путём решения задач программирования (линейного, нелинейного, целочисленного) либо с использованием эвристических методов (генетические и эволюционные алгоритмы). В достаточно редких случаях для расчёта коэффициентов в нашем распоряжении могут быть формулы, гарантирующие получения оптимума (такие формулы даёт, например, Метод Наименьших Квадратов, который мы обсудим в главе про регрессии).

Очевидно, что рассмотреть все возможные целевые функции в рамках одной статьи невозможно, да и не имеет никакого смысла. Чаще всего нас интересует минимальное расстояние между точками и линиями, которое, очевидно, можно оценить по-разному.

Рассмотрим подробней самые простые и популярные в прогнозировании методы оценки коэффициентов моделей.

x <- rnorm(100,100,15)
y <- rep(NA,100)
y[1:95] <- 50 + 0.9 * x[1:95] + rnorm(95,0,5)
y[96:100] <- 190 + 0.2 * x[96:100] + rnorm(5,0,2)

data <- as.data.frame(matrix(NA,100,2))
colnames(data) <- c("x","y")
data[,1] <- x
data[,2] <- y

C <- rep(NA,2)

MSE

MSE расшифровывается как «Mean Squared Error» и переводится как «Средняя квадратическая ошибка». Суть метода заключается по сути в том, чтобы минимизировать сумму квадратов отклонений фактических значений от расчётных (SSE - «Sum of Squared Errors»). Если полученную сумму разделить на число наблюдений, то получится та самая MSE. Формула целевой функции в этом случае выглядит следующим образом:

\begin{equation} \label{eq:estim_MSE}
MSE = \frac{1}{T} \sum_{t=1}^T e_t^2 = \frac{1}{T} \sum_{t=1}^T (y_t -\hat{y}_t)^2 .
\end{equation}

Если бы в формуле \eqref{eq:estim_MSE} не было квадрата, то положительные и отрицательные отклонения друг друга погашали, из-за чего минимизировалось бы не расстояние между фактическими и расчётными значениями, а чёрт знает что. То есть наличие квадратов позволяет получить некоторую оценку расстояния от фактических значений до линии (расчётных значений).

Стоит отметить, что, как мы помним из «Статистического анализа», возведение в квадрат существенно увеличивает те значения, которые лежат далеко от всех остальных. Например, если продажи мороженого колеблются в основном в районе ста штук, но есть наблюдение в 200, то это наблюдение будет тянуть на себя одеяло — влиять существенно на оценки коэффициентов. То есть MSE является не робастной величиной и вообще позволяет получить некоторую среднюю оценку (в среднем фактическое значение \(y_t\) будет соответствовать \(\hat{y}_t\) при данном значении \(x_t\)).

В случае с регрессиями использование MSE соответствует расчёту коэффициентов методом наименьших квадратов, к которому мы обратимся позже.

CF <- function(C){
  residuals <- data[,2] - (C[1] + C[2] * data[,1])
  return(mean(residuals^2))
}

result <- nlminb(c(1,1),CF)
C <- result$par

plot(data)
abline(a=C[1], b=C[2], col="red")

MAE

MAE расшифровывается как «Mean Absolute Error», что с зарубежного на отечественный переводится как «Средняя абсолютная ошибка». Рассчитывается она так:

\begin{equation} \label{eq:estim_MAE}
MAE = \frac{1}{T} \sum_{t=1}^T |e_t| = \frac{1}{T} \sum_{t=1}^T |y_t -\hat{y}_t| .
\end{equation}

Модули в формуле \eqref{eq:estim_MAE} всё так же позволяют избавиться от знаков и получить некоторую оценку расстояния от фактических до расчётных значений, которое нужно будет потом минимизировать. Несомненным преимуществом MAE является то, что модули не увеличивают в разы отклонения, считающиеся выбросами. Поэтому эта оценка является более робастной, чем MSE и фактически соответствует медиане (в 50% случаев при данном значении \(x_t\) зависимая величина \(y_t\) будет не меньше полученной \(\hat{y}_t\)).

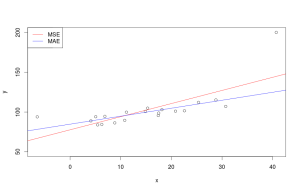
Разница между оценками коэффициентов, полученными при использовании MSE и MAE, наглядно показана на следующем рисунке:

Модели, оценённые с использованием MSE и MAE.

Из-за наличия аномального объёма продаж мороженного при 40 градусах по цельсию, красная линия (соответствующая регрессии, оценённой с помощью MSE) задирается и хуже описывает все остальные нормальные значения. Синяя же линия (соответствующая MAE) демонстрирует больше адекватности, так как в значительно меньшей степени реагирует на творящееся во время такой дикой жары безобразие на улицах города.

CF <- function(C){
  residuals <- data[,2] - (C[1] + C[2] * data[,1])
  return(mean(abs(residuals)))
}

result <- nlminb(c(1,1),CF)
C <- result$par

abline(a=C[1], b=C[2], col="blue")

Квантильные оценки

Прозорливые читатели уже, наверно, догадались, что помимо получения средней и медианной величин, можно так же получить и квантильные. В статистическом анализе регрессии, оценённые таким методом, называются «квантильными регрессиями».

Целевая функция, соответствующая таким квантильным оценкам, имеет вид:

\begin{equation} \label{eq:estim_Quantiles}
CF_\alpha = (1 - \alpha) \sum_{y_t < \hat{y}_t } |e_t| + \alpha \sum_{y_t \geq \hat{y}_t } |e_t| . \end{equation} где \(\alpha\) - это выбранная частота для квантиля (см. «Статистический анализ»), которая в данном случае выступает в роли веса, задаваемому тем или иным суммам. Если \(\alpha>0.5\), то вторая сумма в правой части \eqref{eq:estim_Quantiles}, соответствующая ситуации, когда фактические значения оказываются больше расчётных, будет получать больший вес. Первая же сумма (в которой все фактические значения меньше расчётных) получит меньший вес. Минимизируя такую сумму мы фактически сдвинем расчётные значения вправо — так, чтобы вторая сумма была как можно меньше. В полученных ошибках модели это будет соответствовать заданному квантилю \(\alpha\).

Условие \(y_t < \hat{y}_t\) может быть заменено на \(e_t < 0\), так как остатки модели связаны с фактическими и расчётными значениями уравнением: \(e_t = y_t - \hat{y}_t\).

Для того, чтобы лучше понять, что происходит, когда мы используем такую функцию, рассмотрим пример с \(\alpha=0.5\). В этом случае формула \eqref{eq:estim_Quantiles} будет преобразована в:

\begin{equation} \label{eq:estim_Quantilesexample_1}
CF_{0.5} = 0.5 \sum_{y_t < \hat{y}_t } |e_t| + 0.5 \sum_{y_t \geq \hat{y}_t } |e_t| . \end{equation} Получается, что суммы имеют одинаковый вес, а значит данная формула может быть легко заменена на следующую: \begin{equation} \label{eq:estim_Quantilesexample_2} CF_{0.5} = \sum_{t=1}^T |e_t| . \end{equation} Минимизация функции \eqref{eq:estim_Quantilesexample_2}, как легко заметить, соответствует минимизации MAE \eqref{eq:estim_MAE}. Просто в MAE мы ещё и делим полученную сумму на число наблюдений, что никак на оценки во время оптимизации не влияет.

В результате использования метода квантильных оценок полученная линия регрессии пройдёт не по середине облака, а выше или ниже него, в зависимости от выбранного значения частоты квантиля \(\alpha\). Использование этого критерия при оценке функций в прогнозировании может быть полезным, например, для построения прогнозных интервалов.

Единственная проблема метода - это сложность его использования в случае малого количества наблюдений в выборке. Действительно, нет никакой возможности однозначно определить, например, 2,5% эмпирический квантиль, если в твоём распоряжении 10 наблюдений, потому что в этой малой выборке ниже этого квантиля будет лежать только \( 10 \cdot 0.025 = 0.25 \) наблюдений. Для того, чтобы методом можно было воспользоваться, в распоряжении исследователя должно быть хотя бы \(\frac{1}{\alpha}\) наблюдений, где \(\alpha\) соответствует левому хвосту распределения (для нашего примера это \( \frac{1}{0.025} = 40 \)).

CF <- function(C){
  residuals <- data[,2] - (C[1] + C[2] * data[,1])
  return((1-alpha) * sum(abs(residuals[residuals<0])) +
            alpha * sum(abs(residuals[residuals>=0])))
}

alpha <- 0.05
result <- nlminb(c(1,1),CF)
C <- result$par

abline(a=C[1], b=C[2], col="darkgreen")

alpha <- 0.95

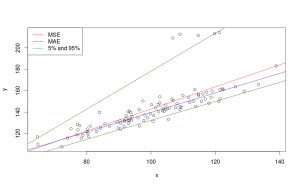
На следующем рисунке изображены линии, соответствующие моделям, оценённым MSE, MAE и 5% и 95% квантилям.

Модели, построенные с помощью MSE, MAE и квантильных оценок

Функция правдоподобия

Все перечисленные выше методы хороши, но сами по себе не имеют этакого статистического обоснования: мы понимаем, как себя будет вести полученная функция, как примерно она пройдёт через наши фактические значения, понимаем, чего можно ожидать в будущем, но мы не можем особо ничего сказать о том, какими будут оценки коэффициентов моделей со статистической точки зрения. Будут ли они получены случайно? Будут ли они стремиться к каким-то значениям, если мы построим модель по другой выборке из тех же данных? А как же быть, если перед нами несколько моделей, описывающих одни и те же данные по-разному? Например, несколько моделей экспоненциального сглаживания, из которых нужно выбрать одну. Или ряд регрессионных моделей... Какой же из них отдать предпочтение и как?

Для ответа на некоторые / все из этих вопросов, нужно обратиться к математической функции под названием "функция правдоподобия" (за бугром эту функцию называют "Likelihood function"). Но сначала нужно немного вспомнить теорию вероятностей. Не переживайте, много вспоминать не придётся. Нужно совсем чуть-чуть.

Итак, предположим, что мы всё ещё имеем дело с мороженным (тем более, что же может быть лучше мороженого? Разве только два мороженых!). В четверг мы замерили уровень продаж и увидели, что он составил 78.5 штук. Любой другой человек просто плюнул бы и продолжил работать дальше. Но пытливому уму статистика может стать интересно, какова вероятность получить такое значение либо значение, лежащее в некоторой области (скажем, от 70 до 80 штук) в случае, если мы предполагаем, что процесс продаж описывается некоторой математической функцией с заданными параметрами (например, простой парной регрессией \eqref{eq:estim_linreg}). Такая вероятность называется условной - то есть вероятность получить определённое значение при выполнении некоторого ряда условий - и записать её математически можно так:

\begin{equation} \label{eq:estim_conditionalprobability}
P(y_t | \theta, \sigma^2)
\end{equation}

где \(\theta\) - это вектор всех наших параметров, \(\sigma^2\) - дисперсия модели. В нашем примере с моделью \eqref{eq:estim_linreg} имеем \(\theta = \begin{pmatrix} a \\ b \end{pmatrix}\).

Зачем же нам эта вероятность, когда нам нужна величина правдоподобия? Всё очень просто. Это самое правдоподобие фактически равно условной вероятности \eqref{eq:estim_conditionalprobability}, но имеет другой смысл: оно показывает, насколько правдоподобны полученные значения параметров при имеющемся фактическом значении продаж. Математически это выражается следующим равенством:

\begin{equation} \label{eq:estim_probabilityandlikelihood}
L(\theta, \sigma^2 | y_t) = P(y_t | \theta, \sigma^2)
\end{equation}

То есть это взгляд на тот же самый процесс, но с другой стороны.

Если теперь рассмотреть совместную вероятность получения параметров при всех имеющихся наблюдениях от \(1 \text{ до } T\), то мы получим следующую функцию правдоподобия (здесь нужно иметь в виду, что при этом предполагается независимость наблюдений):

\begin{equation} \label{eq:estim_generallikelihood}
L(\theta, \sigma^2 | Y) = \prod_{t=1}^T P(y_t | \theta, \sigma^2) ,
\end{equation}

где \(Y\) - это вектор всех фактических значений: \(Y = \begin{pmatrix}y_1 \\ y_2 \\ \vdots \\ y_T \end{pmatrix}\)

Теперь мы можем подставлять в \eqref{eq:estim_generallikelihood} разные значения параметров модели \(\theta \text{ и } \sigma^2 \) и получать разные вероятности. Естественно, обычно мы заинтересованы в том, чтобы вероятность была максимальной, так что функцию правдоподобия \eqref{eq:estim_generallikelihood} можно максимизировать, задавая разные значения параметров, и получить какие-нибудь оптимальные оценки коэффициентов.

Всё. Счастье есть! Можно откинуться на спинку стула и потягивать чай / мохито / виски / ром - в зависимости от времени года и предпочтений прогнозиста.

Однако теперь возникает другой вопрос: как же нам получить условные вероятности, использующиеся в \eqref{eq:estim_generallikelihood}? А здесь как раз вступают в силу различные предположения, которые исследователь обычно накладывает относительно модели. Одно из самых популярных предположений - это то, что остатки модели распределены нормально. Оно теоретически оправдано в тех случаях, когда в нашей модели учтены все существенные переменные, а сама модель правильно специфицирована. То есть по сути мы говорим о том, что смогли угадать, что собой представляет идеальная модель. В этом случае вместо вероятности мы можем спокойно использовать функцию плотности нормального закона распределения вероятностей (который так любят все: и взрослые, и дети). Напоминаю, сама функция нормального распределения выглядит примерно так:

\begin{equation} \label{eq:estim_normaldensity}
P(y_t | \theta, \sigma^2) = \frac{1}{\sqrt{2 \pi \sigma^2}} e ^{-\frac{e_t^2}{2\sigma^2}},
\end{equation}

где \(e_t = y_t - \hat{y}_t\).

Подставляя \eqref{eq:estim_normaldensity} в \eqref{eq:estim_generallikelihood}, мы получим следующую функцию правдоподобия на основе нормального распределения:

\begin{equation} \label{eq:estim_likelihoodnormal}
L(\theta, \sigma^2 | Y) = \prod_{t=1}^T \frac{1}{\sqrt{2 \pi \sigma^2}} e ^{-\frac{e_t^2}{2\sigma^2}} = \left( 2 \pi \sigma^2 \right)^{-\frac{T}{2}} e ^ {\left( -\frac{1}{2} \sum_{t=1}^T \frac{e_t^2}{\sigma^2}\right)} .
\end{equation}

Очевидно, что функцию \eqref{eq:estim_likelihoodnormal} неудобно максимизировать в таком её виде, так как приходится сталкиваться с произведениями и экспонированием. Однако оптимальное значение коэффициентов не изменится, если мы линеаризуем эту функцию (например, прологарифмируем левую и правую части, используя натуральный логарифм). В этом случае мы получим следующую функцию (которая у них там на западе называется "log-likelihood"):

\begin{equation} \label{eq:estim_loglikelihoodnormal}
\ell(\theta, \sigma^2 | Y) = \ln ( L(\theta, \sigma^2 | Y) ) = -\frac{T}{2} \ln \left( 2 \pi \sigma^2 \right) -\frac{1}{2} \sum_{t=1}^T \frac{e_t^2}{\sigma^2} .
\end{equation}

В правой части \eqref{eq:estim_loglikelihoodnormal} дисперсию можно вынести за знак суммы, так как она представлена константой, тогда получим:

\begin{equation} \label{eq:estim_loglikelihoodnormal1}
\ell(\theta, \sigma^2 | Y) = -\frac{T}{2} \ln \left( 2 \pi \sigma^2 \right) -\frac{1}{2 \sigma^2} \sum_{t=1}^T e_t^2 .
\end{equation}

Теперь можно попытаться математически вывести при каком значении параметров функция будет максимизироваться. Проще всего это сделать вначале с дисперсией. Для этого возьмём первую производную \eqref{eq:estim_loglikelihoodnormal1} по \(\sigma^2\) и приравняем её к нулю:

\begin{equation} \label{eq:estim_loglikelihoodnormaldsigma1}
\frac{d \ell(\theta, \sigma^2 | Y)}{d \sigma^2} = -\frac{T}{2} \frac{2 \pi 2 \sigma}{ 2 \pi \sigma^2 } + 2 \frac{1}{2 \sigma^3} \sum_{t=1}^T e_t^2 = 0.
\end{equation}

Если теперь в \eqref{eq:estim_loglikelihoodnormaldsigma1} сократить то, что сокращается и перенести правое слагаемое в правую часть, то получим:

\begin{equation} \label{eq:estim_loglikelihoodnormaldsigma2}
\frac{T}{\sigma} = \frac{1}{\sigma^3} \sum_{t=1}^T e_t^2.
\end{equation}

Умножим теперь левую и правую части \eqref{eq:estim_loglikelihoodnormaldsigma2} на \(\sigma^3\) и разделим на \(T\):

\begin{equation} \label{eq:estim_loglikelihoodnormalsigma}
\sigma^2 = \frac{1}{T} \sum_{t=1}^T e_t^2.
\end{equation}

Полученная формула позволяет нам оценить дисперсию ошибок по выборке с помощью статистически выверенного и корректного метода - путём максимизации функции правдоподобия на основе нормального закона распределения вероятностей. Ничего нового нам эта формула, вроде бы, не даёт, потому что мы итак знаем, как рассчитать дисперсию ошибок, но нам она полезна как раз с точки зрения статистического обоснования. Однако, чтобы не перепутать, что мы вообще-то имеем дело не с истинной дисперсией (существующей в генеральной совокупности и воображении статистиков), а с оценённой по выборке, мы будем полученную с помощью \eqref{eq:estim_loglikelihoodnormalsigma} дисперсию обозначать \(\hat{\sigma}^2\). Кроме того, отметим, что мы только что показали, что дисперсия, оценённая по формуле \eqref{eq:estim_loglikelihoodnormalsigma} является некой оптимальной оценкой только в случае, если мы имеем дело с нормальным распределение ошибок!

Что ж, продолжим наши пляски с бубном и подставим эту оценённую дисперсию в \eqref{eq:estim_loglikelihoodnormal1}. Пойдём ещё дальше и подставим сразу значение из формулы \eqref{eq:estim_loglikelihoodnormalsigma}:

\begin{equation} \label{eq:estim_concentratedloglikelihoodnormal}
\ell(\theta | Y) = -\frac{T}{2} \ln \left( 2 \pi \frac{1}{T} \sum_{t=1}^T e_t^2 \right) -\left({2 \frac{1}{T} \sum_{t=1}^T e_t^2}\right)^{-1} \sum_{t=1}^T e_t^2 .
\end{equation}

Заметим, пока не поздно, что функция правдоподобия, в которой используется оценённая дисперсия, называется "концентрированной" ("concentrated log-likelihood").

В \eqref{eq:estim_concentratedloglikelihoodnormal} суммы в правой части легко сокращаются, а произведение под знаком логарифма легко преобразуется в сумму логарифмов таким вот образом:

\begin{equation} \label{eq:estim_concentratedloglikelihoodnormal1}
\ell(\theta | Y) = -\frac{T}{2} \ln \left( 2 \pi \right) -\frac{T}{2} \ln \left( \frac{1}{T} \sum_{t=1}^T e_t^2 \right) - \frac{T}{2} .
\end{equation}

После ряда элементарных перестановок можно получить следующую, ещё более простую, логарифмированную концетрированную функцию правдоподобия:

\begin{equation} \label{eq:estim_concentratedloglikelihoodnormal2}
\ell(\theta | Y) = -\frac{T}{2} \left( \ln \left( 2 \pi e \right) + \ln \left( \frac{1}{T} \sum_{t=1}^T e_t^2 \right) \right) .
\end{equation}

Максимизировать функцию \eqref{eq:estim_concentratedloglikelihoodnormal2} теперь очень просто. На самом деле ещё легче - минимизировать \(-\frac{2}{T} \ell(\theta | Y)\), так как размер выборки у нас фиксирован. \eqref{eq:estim_concentratedloglikelihoodnormal2} тогда преобразуется в:

\begin{equation} \label{eq:estim_concentratedloglikelihoodnormalnegative}
-\frac{2}{T} \ell(\theta | Y) = \ln \left( 2 \pi e \right) + \ln \left( \frac{1}{T} \sum_{t=1}^T e_t^2 \right) .
\end{equation}

Ну, и в качестве финального аккорда, можно избавиться от константы \(\ln \left( 2 \pi e \right)\), так как она никак не влияет на получение оптимальных коэффициентов. А полученное в итоге число можно вообще проэкспонировать, для того, чтобы прийти к следующей целевой функции, минимизируя которую мы будем получать оценки максимального правдоподобия (не забываем про допущение о нормальном распределении остатков модели):

\begin{equation} \label{eq:estim_concentratedloglikelihoodnormal4}
CF = \frac{1}{T} \sum_{t=1}^T e_t^2 .
\end{equation}

Удивительным образом эта целевая функция целиком и полностью соответствует MSE (формула \eqref{eq:estim_MSE}).

В этом месте может возникнуть вопрос: зачем же все эти выводы и сложные процедуры, если мы в итоге получили всего лишь известный нам критерий MSE? Ответов на этот вопрос несколько:

1. Путём простых математических выкладок мы доказали, что MSE является эффективным критерием оценки коэффициентов моделей в том случае, если остатки модели распределены нормально. Например, для наших примеров в предыдущих параграфах (см. рисунок с MSE и MAE) эта предпосылка нарушается, поэтому MSE не является эффективным критерием.
2. Используя логарифмированную концентрированную функцию правдоподобия \eqref{eq:estim_concentratedloglikelihoodnormal2} можно осуществлять выбор наилучшей модели из ряда имеющихся в распоряжении исследователя. Эту тему мы обсудим подробней в одном из следующих параграфов.
3. Кроме того, всё та же функция позволяет нам получать оценки дисперсий коэффициентов любой модели. Они нам могут понадобиться для проверки всяких статистических гипотез или построения доверительных интервалов. Для получения этих дисперсий нужно обратиться к некой вещи под названием "Информация Фишера", но здесь мы вдаваться в детали пока не будем.
4. Если нам не нравится предположение о нормальности распределения остатков, мы можем использовать любую другую функцию распределения в \eqref{eq:estim_generallikelihood}. Конечно же, придётся произвести все последующие выводы аналогично тем, что мы произвели только что (а в некоторых случаях ничего такого сделать и не получится, функцию придётся максимизировать как есть), но зато это даст нам красивые, статистически выверенные оценки.
5. Используя этот подход, можно показать, что минимизация MAE является оптимальным методом оценки в случае, если остатки имеют распределение Лапласа, а квантиальные оценки дают максимум функции правдоподобия для асимметричного распределения Лапласа.

На этом простые методы оценки параметров моделей заканчиваются. В следующей статье мы перейдём к продвинутым.