В предыдущих статьях мы рассматривали обычно два аспекта функции es(): теорию, лежащую в основе, а затем практику. Однако в этой статье первую часть мы опустим, потому что рассказывать тут не о чем. Данная статья по большей части посвящена тому, что же ещё можно натворить с помощью параметров функции es().

Начнём с инициализации экспоненциального сглаживания.

История экспоненциального сглаживания насчитывает дюжины методов задания стартовых значений. Некоторые работают вполне себе неплохо, другие в корне неправильны. Некоторые из них позволяют сохранять данные, в то время как другие уменьшают размер выборки, с которой работает исследователь. В es() инициализация экспоненциального сглаживания сделана до начала выборки. То есть вектор \(v_t\), к которому который мы обращались в предыдущих статьях, задаётся в функции до первого наблюдения \(y_1\). Это вполне себе согласуется с подходом Hyndman et al. 2008, и в этом случае мы не теряем наблюдения. Тем не менее, само стартовое значение может быть задано в функции по-разному.

1. Оптимизация. Этот метод означает, что стартовое значение будет подобрано с помощью оптимизатора во время поиска постоянной сглаживания. То есть число параметров, которые нужно оценить, в этом случае увеличивается. Это стандартный метод инициализации в es() и задаётся он параметром initial=»optimal».

Если оптимизация работает вполне хорошо на месячных данных, то это, к сожалению, не означает, что она так же будет хорошо работать и на данных с более высокой частотностью (например, недельных или дневных). Причиной тому высокое число параметров для подбора. Например, для построения какой-нибудь модели ETS(M,N,M) на недельных данных нужно оценить 52 + 1 + 2 + 1 = 56 параметров (52 сезонных коэффициента, 1 значение для компоненты уровня ряда, 2 постоянных сглаживания и 1 дисперсию остатков). Это непростая задача, и не всегда удаётся её эффективно решить. Поэтому нам могут пригодиться другие методы инициализации ETS.

Посмотрим, что получается, когда мы сталкиваемся с этой проблемой на каком-нибудь примере. Вот, например, ряд taylor из пакета forecast. Это получасовые данные по спросу на электроэнергию. Частота этих данных — 336 (7 дней недели * 48 получасов в сутках). Оценить такое количество параметров достаточно сложно. Тем не менее, посмотрим, что получится, если мы используем стандартную оптимизацию в функции es() с автоматическим выбором моделей:

es(taylor,"ZZZ",h=336,holdout=TRUE)

Forming the pool of models based on... ANN, ANA, ANM, AAA, Estimation progress: 100%... Done!
Time elapsed: 18.47 seconds
Model estimated: ETS(ANA)
Persistence vector g:
alpha gamma 
0.850 0.001 
Initial values were optimised.
340 parameters were estimated in the process
Residuals standard deviation: 250.546
Cost function type: MSE; Cost function value: 56999

Information criteria:
     AIC     AICc      BIC 
51642.90 51712.02 53756.01 
Forecast errors:
MPE: 1%; Bias: 50%; MAPE: 1.8%; SMAPE: 1.8%
MASE: 0.798; sMAE: 1.8%; RelMAE: 0.078; sMSE: 0.1%

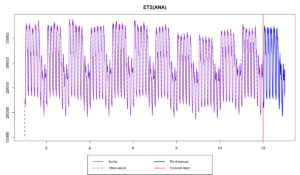
Как говорит нам функция, нам пришлось оценить 340 параметров, а выбор модели занял 18 секунд (при этом было проверено только 5 моделей). В итоге у нас получилось что-то вот такое:



Спрос на электроэнергию и модель ETS(A,N,A), инициализированная с помощью оптимизации

Первое, что обращает на себя внимание, это те самые стартовые значения из-за которых первые расчётные значения оказались совершенно неадекватными. Это как раз из-за высокого числа параметров. Неточные стартовые значения — это плохо, потому что в итоге мы можем выбрать не ту модель (так как все остальны будут инициализированы ещё хуже). Поэтому стоит обратиться к другим методам инициализации.

2. «Backcasting», что-то типа прогноза назад. Это второй метод задания стартовых значения для компонент ETS. В этом случае модель строится несколько раз, используя следующую формулу для построения вперёд:

\begin{equation} \label{eq:ETSANN_Forward}
\begin{matrix}
y_t = l_{t-1} + \epsilon_t \\
l_t = l_{t-1} + \alpha \epsilon_t
\end{matrix}
\end{equation}
и вот такую, когда получен финальный прогноз:
\begin{equation} \label{eq:ETSANN_Backward}
\begin{matrix}
y_t = l_{t+1} + \epsilon_t \\
l_t = l_{t+1} + \alpha \epsilon_t
\end{matrix}
\end{equation}

То есть в формуле \eqref{eq:ETSANN_Forward} для расчёта следующего значения мы используем предыдущее, в то время как в формуле \eqref{eq:ETSANN_Backward} мы рассчитываем предыдущее на основе следующего. Первую мы используем при расчёте значение с начала выборки до самого её конца, затем разворачиваемся и используем вторую, с конца в начало. Это позволяет уточнить стартовое значение и сделать его близким к самой модели. В функции es() эта процедура повторяется три раза и может быть вызвана параметром initial=»backcasting». Как и упомянуто ранее, эта процедура рекомендуется при работе с недельными, дневными, часовыми и прочими видами сезонности.

Для примера возьмём всё тот же ряд из пакета forecast:

es(taylor,"ZZZ",h=336,holdout=TRUE,initial="b")

В этот раз процедура заняла около семи секунд:

Forming the pool of models based on... ANN, ANA, ANM, AAA, Estimation progress: 100%... Done! 
Time elapsed: 6.81 seconds
Model estimated: ETS(MNA)
Persistence vector g:
alpha gamma 
    1     0 
Initial values were produced using backcasting.
3 parameters were estimated in the process
Residuals standard deviation: 0.007
Cost function type: MSE; Cost function value: 38238

Information criteria:
     AIC     AICc      BIC 
49493.46 49493.47 49512.11 
Forecast errors:
MPE: 0.8%; Bias: 40.6%; MAPE: 1.7%; SMAPE: 1.8%
MASE: 0.784; sMAE: 1.7%; RelMAE: 0.076; sMSE: 0.1%

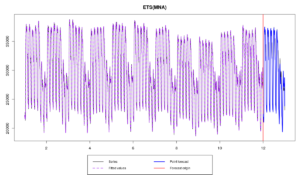
Функция проверила всё тот же пул моделей и выбрала ETS(M,N,A), оценив всего три параметра вместо 340. Мы в итоге получили странную модель, в которой постоянная сглаживания уровня ряда оказалась равной единице (что соответствует процессу случайного блуждания для уровня), а постоянная сглаживания для сезонности — равной нулю (что означает, что мы имеем дело с детерминированной сезонной компонентой).

В итоге выглядит это всё вот так:



Спрос на электроэнергию и модель ETS(M,N,A), инициализированная с помощью backcasting

Как видим, «backcasting» — это неплохой метод инициализации, который может быть полезен в тех случаях, когда мы имеем дело с высокочастотными данными. Более того, где-то в глубине этих ваших интернетов есть доказательство того, что эта техника асимптотически даёт такие же значения, как и метод наименьших квадратов. Это по сути означает, что метод (1) и метод (2) по мере увеличения числа наблюдений сходятся друг с другом в оценках парметров.

3. Произвольные значения. Если по какой-то причине нам известны стартовые значения (либо из предыдущих экспериментов, либо из похожих данных), то мы можем передать их функции es() в виде вектора. В этом случае нам помогут параметры initial и initialSeason. Функция в этом случае использует эти значения и построит модель, оценивая только постоянные сглаживания. Мы можем предоставить как оба параметра, так и только один из них — в зависимости от стоящей перед нами задачи, функция оценит всё недостающее сама. В случае, если мы работаем с несезонной моделью предоставлять initialSeason ненужно. Заметим, что использовать backcasting в случае с заданием произвольных значений не получится, функция всегда будет использовать оптимизацию, если что-то ей недодали. Ещё одно важное замечание — выбор модели и комбинирование прогнозов не работает с этим методом инициализации.

Продолжая наши пример, мы используем классическую декомпозицию для построения модели ETS(M,N,M) по ряду taylor:

ourFigure <- decompose(taylor,type="m")$figure
es(taylor,"MNM",h=336,holdout=TRUE,initial=mean(taylor),initialSeason=ourFigure)

Можно даже сравнить этот метод с двумя другими:

es(taylor,"MNM",h=336,holdout=TRUE,initial="o")
es(taylor,"MNM",h=336,holdout=TRUE,initial="b")

Построение модели в этом случае у меня занимает что-то порядка четырёх секунд, в то время как на initial="o" нужно потратить 13, а для initial="b" — около семи. Итоговые модели выглядят очень похоже.

Этот, третий, метод инициализации может быть полезен, если по какой-то причине предыдущие два недоступны (например, нам нужно что-то посчитать быстро и на большом числе рядов данных) и в нашем распоряжении уже имеются стартовые значения. Его можно также использовать для научных экспериментов. Во всех остальных случаях я бы его не рекомендовал к использованию.

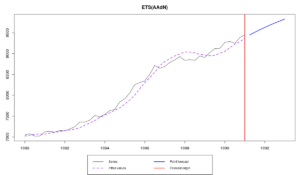
В функции es() есть и другие увлекательные параметры. Например, параметр persistence позволяет задавать вектор с постоянными сглаживаниями, которые должны по длине соответствовать числу компонент модели (они иду в порядке: уровень, тренд, сезонность), а параметр phi позволяет задавать значения для параметра демпфирования тренда. Так, например, модель ETS(A,Ad,N), может быть построена по какому-нибудь ряду N1234 из M3 с произвольными заданными значениями:

es(M3$N1234$x,"AAdN",h=8,persistence=c(0.2,0.1),phi=0.95)

Сравнить этот график:

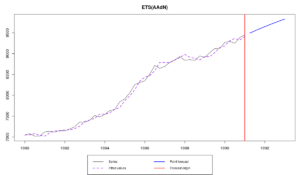
с полученным, если эти значения не задавать:

es(M3$N1234$x,"AAdN",h=8)

Естественно, задавать параметры вручную стоит только в том случае, если вам уж невтерпёж, и у вас есть какие-то основания для этого. В противном случае используйте оптимизацию и не выпендривайтесь не задумывайтесь об этом.

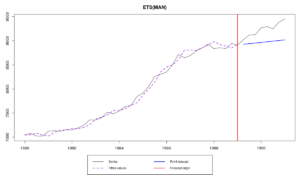
Ещё одна крутая вещь в функции es() - это то, что она сохраняет все упомянутые выше значения и возвращает их в виде списка вместе со многими другими полезными параметрами. Например, выберем наилучшую модель по ряду N1234 и сохраним её:

ourModel <- es(M3$N1234$x,"ZZZ",h=8,holdout=TRUE)

Получиться должен вот такой график:

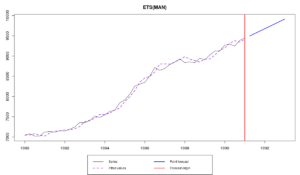
А теперь используем маленькую, но гордую функцию model.type() (которая вытаскивает тип модели из сохранённых объектов) и используем точно такую же модель, с теми же параметрами, но уже с большим числом наблюдений в выборке:

es(M3$N1234$x,model.type(ourModel),h=8,holdout=FALSE,initial=ourModel$initial,persistence=ourModel$persistence,phi=ourModel$phi)

Теперь мы получим ту же самую модель, но с обновлёнными значениями компонент на основе последних восьми наблюдений:

На самом деле существует и более простой способ сделать то же самое - для этого достаточно в параметр model передать нашу модель ourModel следующим образом:

es(M3$N1234$x,model=ourModel,h=8,holdout=FALSE)

Таким образом мы, например, можем произвести прогнозы методом сдвигающейся точки для выбора наиболее точной прогнозной модели.

Функция model.type() также работает с функцией ets() из пакета forecast. Так что вы можете, например, использовать функцию ets(), а после сконструировать модель того же типа с помощью es():

etsModel <- ets(M3$N1234$x)
es(M3$N1234$x,model=model.type(etsModel),h=8,holdout=TRUE)

Фух! На сегодня всё. Надеюсь, эта статья помогла вам узнать функцию es() получше, и теперь вам будет чем заняться, когда нечем заняться… До новых встреч!