Данная статья многим может показаться совершенно непонятной. Оно и не удивительно, к моделям экспоненциального сглаживания мы ещё в учебнике не подобрались, а вот программу для них уже обсуждаем… Что же поделаешь?! Жизнь жестока!

Итак, в R для построения моделей экспоненциального сглаживания существует прекрасная функция ets() из пакета forecast, которым занимается Rob J.Hyndman. Пакет находится в общих репозиториях и легко устанавливается командой в R:

install.packages("forecast")

Однако у этой функции с моей точки зрения есть несколько недостатков, среди которых можно выделить следующие:

1. Отсутствие некоторых моделей экспоненциального сглаживания;

В книге «Forecasting with Exponential Smoothing» Роб с соавторами предлагают таксономию, в соответствии с которой существует всего 30 моделей экспоненциального сглаживания, однако функция ets() позволяет строить только 19 из них, опуская сложные в оценке модели (включая оригинальную модель Хольта-Уинтерса).

2. Отсутствие возможности задавать произвольные значения компонент;

Для инициализации любой модели экспоненциального сглаживания нужно задать самое первое расчётное значение либо первые значения компонент уровня ряда, тренда и сезонной составляющей. В ets() они подбираются во время оптимизации, но иногда стартовые значения имеет смысл задать вручную. Именно этой возможности в ets() и нет.

3. Невозможность включения экзогенных (внешних) переменных;

В той же книге обсуждается, что в модель пространства состояний, в виде которой авторы представляют любое экспоненциальное сглаживание, можно легко включить произвольное количество экзогенных переменных, которые объяснили бы поведение нашего показателя в некоторые моменты времени. Однако возможность включения переменных в функции ets() отсутствует. Пока она отсутствует и в моей функции «es», но в списке приоритетов она не на последнем месте.

4. Ограниченность критериев в целевой функции

ets() позволяет оценивать модели, используя либо простую сумму квадратов отклонений, либо функцию правдоподобия, либо среднюю абсолютную ошибку… Но траекторных критериев в функции нет. Под траекторными понимаются такие критерии, которые учитывают прогнозную траекторию модели и минимизируют ошибку не на один шаг вперёд, а на несколько.

5. Отсутствие возможности разбиения выборки на тестовую и проверочную.

Иногда нам нужно просто проверить, как себя поведёт та или иная функция на выбранном ряде данных. Для того, чтобы сопоставить фактические значения с прогнозными с помощью функции ets() нужно сделать много лишних движений.

Этих недостатков мне показалось достаточно для того, чтобы написать свою функцию, но главной проблемой моей функции всё это время была скорость работы. Недавно я переписал главные куски кода в C++, и теперь скорость выросла в разы (порядка 30 раз). Теперь мне за свою функцию не стыдно и можно о ней немного рассказать.

Установить функцию можно легко если в вашем R есть пакет «devtools» (мы это уже кратко обсуждали в статье про CES). Однако при сборке под Windows вам может понадобиться программа под названием «Rtools». Скачать её можно отсюда, устанавливать лучше в корневой каталог. Так же для сборки понадобятся пакеты Rcpp и RcppArmadillo:

install.packages("Rcpp")
install.packages("RcppArmadillo")

В случае возникновения проблем, рекомендую просмотреть статью про основы R.

После этого установка пакета с функцией es() (от английского «Exponential Smoothing») выполняется следующей командой:

devtools::install_github("trnnick/TStools")

В этот репозиторий я загружаю уже протестированные функции, а всё самое весёлое и потенциально плохо работающее я загружаю в свой пакет «prognosis». Если вы смелый, ловкий, умелый, то милости прошу установить пакет «prognosis».

После установки подключим пакет в R:

library("TStools")

А теперь посмотрим, что нам даёт эта функция es(). Возьмём для примера какой-нибудь ряд из базы M3. Например, N1234. Для того, чтобы сравнить прогнозные и фактические значения на проверочной выборке, предварительно объединим тестовую и проверочную части в одну переменную \( y \):

y <- ts(c(M3$N1234$x,M3$N1234$xx),frequency=frequency(M3$N1234$x),start=start(M3$N1234$x))

И для начала попросим функцию самостоятельно выбрать наилучшую модель экспоненциального сглаживания и дать прогноз на 8 наблюдений вперёд.

es(y,h=8,holdout=TRUE)->test

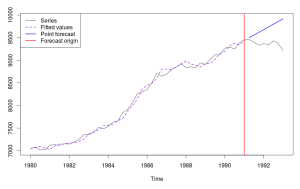
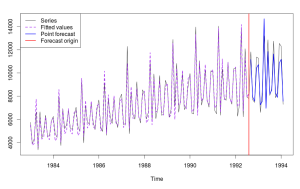
В результате этого получим следующий график:

и вывод в консоль:

Building model: ANN AAN AAdN AMN AMdN ANA AAA AAdA AMA AMdA ANM AAM AAdM AMM AMdM MNN MAN MAdN MMN MMdN MNA MAA MAdA MMA MMdA MNM MAM MAdM MMM MMdM ... Done! 
"Time elapsed: 4.04 seconds"
"Model constructed: MAN"
"Persistence vector: 0.672, 0.233"
"Initial components: 7036.588, 7.801"
"Residuals sigma: 0.008"
"CF type: one step ahead; CF value is: 4677"
"Biased log-likelihood: -258"
"AIC: 515.97 AICc: 516.97"
"MASE: 4.82"
"MASALE: 3.72%"

Разберём построчно, что же мы тут получили.

В первой строке перечислены все опробованные модели, и слова в ней добавляются по мере построения модели.

В строке [2] показано время, потраченное на работу программы. Эта информация позволяет нам прикинуть, сколько может занять работа программы по массиву похожих временных рядов. 8 секунд - это, конечно, немало. Надеюсь, в будущем я смогу ещё оптимизировать код и довести этот показатель до 2 - 3 секунд.

Строка [3] показывает выбранную функцией модель. Это модель с аддитивной ошибкой, аддитивным трендом, без сезонности. Этой модели соответствует метод Хольта.

Строкой [4] перечислены оптимальные постоянные сглаживания, которые функция es получила в ходе расчётов.

[5] - это стартовые значения компонент уровня и тренда в модели Хольта.

[6] - это стандартное отклонение остатков полученной модели.

В строке [7] написано, какой критерий использовался при оценке. "One step ahead" соответствует минимизации средней квадратической одношаговой прогнозной ошибки. Подробней о критериях скоро можно будет прочитать в готовящейся к публикации статье "Методы оценки параметров моделей" в разделе Инструментарий прогнозиста.

CF value в той же строе [7] - это значение полученной целевой функции. Особо полезной информации не несёт, но позволяет проводить элементарное сравнение между моделями, построенными по одному и тому же ряду данных.

[8] Biased log-likelihood - смещённое значение логарифмированной функции правдоподобия. Техническая деталь, не несущая особой пользы человечеству. Будет убрана в следующем релизе.

Информационные критерии AIC и AICc в строке [9] позволяют проводить более корректно сравнение между моделями. Общий принцип - чем меньше значение, тем ближе модель к некой "истинной", лежащий где-то там, в основе мироздания. Для модели ETS(M,A,N), как видим, получились такие вот значения. Для сравнения, для сезонной модели ETS(A,A,A), построенной по этому же ряду, у меня получились такие значения: "AIC: 526.862 AICc: 532.005". Это говорит о том, что модель ETS(M,A,N) ближе к истине, чем ETS(A,A,A), что неудивительно - в нашем ряде данных сезонности нет. Информационные критерии мы ещё обсудим в будущем параграфе "Выбор прогнозной модели" раздела "Инструментарий прогнозиста".

Пунктами [10] и [11] показаны ошибки прогноза. Первая - это "Mean Absolute Scale Error", а вторая - такая же, отличающаяся лишь знаменателем в формуле. Чем меньше значение, тем точнее оказался прогноз. Подробней о них мы поговорим во всё том же разделе "Инструментарий прогнозиста". Но не сегодня.

Но и это ещё не всё. Переменная test, в которую мы сохранили результаты работы нашей функции, содержит в себе кучу всего интересного (вызываемого командой вида test$var, где var - это имя переменной):

• persistence - вектор постоянных сглаживания. Может содержать от 1 до 3-х следующих элементов: \(\alpha, \beta, \gamma \).
• phi - значение коэффициента демпфирования. Имеет смысл только в случае, если построена модель с демпфированным трендом.
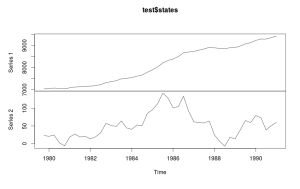
• states - матрица, содержащая компоненты экспоненциального сглаживания. В случае с нашей моделью ETS(A,A,N) содержит 2 столбца: уровень и тренд. Её можно так же представить графически следующим образом:

  plot(test$states)
  

  Должен получиться вот такой график:

  

  Компоненты модели ETS(M,A,N) по ряду N1234 в динамике

• fitted - расчётные значения в тестовой выборке.
• forecast - прогноз по модели (соответствующий проверочной выборке).
• residuals - остатки модели, соответствующие одношаговым ошибками, полученным по тестовой выборке.
• errors - матрица ошибок модели. В случае, если использовался стандартный критерий "One step ahead" совпадает с остатками residuals. В случае с другими критериями содержит итоговую матрицу многошаговых ошибок.
• x - исходный ряд данных (весь ряд, отправленные функции).
• ICs - информационные критерии AIC и AICc, рассчитанные для модели.
• CF - значение целевой функции.
• FI - матрица "информация Фишера". Получается из функции правдоподобия и нужна для расчёта дисперсий коэффициентов. В R ковариационную матрицу коэффииентов на основе неё можно легко получить с помощью следующей команды:

  solve(-test$FI)
  

Мы можем попросить es() построить нам какую-нибудь конкретную модель экспоненциального сглаживания, а не выбранную автоматически. Для этого надо передать функции название модели. Например, для модели демпфированного тренда ETS(A,Ad,N) нужно ввести:

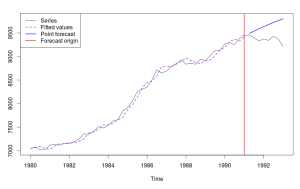
es(y,model="AAdN",h=8,holdout=TRUE)->test

Вывод в консоль будет аналогичным предыдущему, а график получится такой:

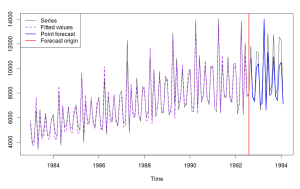
es() может построить и всякие "запрещённые" в ets() модели. Например, по ряду N2568 самой близкой к "идеальной" будет модель ETS(A,Ad,M), которая соответствует методу Хольта-Уинтерса и в ets() недоступна. Выглядит это графически вот так:

es() так же может находить параметры из классических и из расширенных границ для постоянных сглаживания. Я лично считаю, что только расширенные границы и нужно использовать при оценке моделей экспоненциального сглаживания, но некоторые прогнозисты со мной не согласны (но мы их со временем переубедим. На нашей стороне правда и Keith Ord). По умолчанию в функции используются классические границы, но расширенные включаются достаточно легко:

y <- ts(c(M3$N2568$x,M3$N2568$xx),frequency=frequency(M3$N2568$x),start=start(M3$N2568$x))
es(y,h=18,holdout=TRUE,bounds="admissible")->test

Вместо слова "admissible" можно ввести и просто первую букву - "a".

Из-за того, что расширенные границы больше классических, во время оптимизации могут получаться другие оптимальные значения параметров. Для нашего сезонного ряда N2568 оптимальной моделью теперь будет ETS(M,A,M), которая позволяет построить более точный прогноз по ряду. Графически это выглядит так:

И вот мы подобрались к самому интересному. Достаточно важной особенностью функции es() является возможность использовать тракеторные целевые функции. По умолчанию используется нечто под названием "TLV" - Total Logarithmic Variation. Суть метода заключается в том, что вместо одношаговой ошибки на каждом наблюдении производится многошаговая (от 1 до h, где h - срок прогнозирования). Затем по этим ошибкам рассчитываются дисперсии, которые логарифмируются, суммируются и минимизируются. На сайте на эту тему есть статья. Напомним, что использование "TLV" позволяет увеличивать точность долгосрочных прогнозов при незначительном уменьшении точности краткосрочных. Помимо TLV есть ещё "GV" - generalised variance, "TV" - Total Variation и "hsteps" - ошибка прогноза на h шагов вперёд. При использовании TLV и GV можно так же легко использовать процедуру выбора наилучшей модели. А вот использование этой процедуры в случаях с TV и hsteps ничем теоретически не обосновано.

Посмотрим, что получится, если использовать траекторную целевую функцию для того же сезонного ряда N2568:

es(y,h=18,holdout=TRUE,trace=TRUE)->test

Оптимальной остаётся всё та же функция ETS(M,A,M), параметры отличаются незначительно, но точность прогноза вырасла - ошибка уменьшилась с 8,71% до 6,37%. А всё из-за того, что во втором случае лучше выявлены долгосрочные тенденции.

Про методы оценки моделей можно почитать здесь, а можно - и просто посмотреть презентацию, которую я делал в Глазгоу - там вкратце описана идея траекторных целевых функций.

Пока по es() всё. Функция всё ещё разрабатывается и дорабатывается. Следите за обновлениями!