Два года назад я написал статью на английском языке про прогнозные ошибки и о том, как можно и как ненужно измерять точность прогнозов. Переводить на русский я её не стал из-за нехватки времени и дублирования частей статьи вот этим постом на русскоязычной версии сайта. Но прошло время, моё понимание проблемы немного изменилось, и я решил написать продолжение статьи. В этот раз я решил перевести продолжение, так как в нём, как мне кажется, есть полезная информация.
Введение
Начнём с того, что в статистике есть понимание, что MSE минимизируется средней величиной, в то время как MAE минимизируется медианой. В сети Интернет можно найти много статей на эту тему. Вот, например, первая, вторая и третья. Они на английском, но по-разному так или иначе объясняют эту идею. Но в связи с этим среди прогнозистов и статистиков иногда возникает недопонимание того, что можно делать, измеряя точность моделей, а чего нельзя.
Во-первых, некоторые аналитики считают, что подобное соотношение применимо только при оценке моделей. По какой-то причине они считают, что оценка точности на проверочной выборке разительно отличается от процесса построения модели. Однако при выборе модели на основе некой ошибки, мы так или иначе накладываем условия на сами прогнозы. Если один метод гарантирует меньшую MAE, чем другой на проверочной выборке, то это означает что его прогноз ближе к медиане данных.
Для того, чтобы лучше понять эту идею, возьмём пример с нулевым прогнозом. В случае с прерывистым спросом (когда спрос происходит не предсказуемо) нулевой прогноз будет наилучшим в соответствии с MAE, особенно, если нулей в данных больше 50%. Причина этого эффекта проста: если ваши данные содержат большое количество нулей, то самый простой и безопасный прогноз — это сказать, что мы ничего в будущем не продадим. Полезность такого прогноза сомнительна, но он будет достаточно точным. Именно поэтому ошибки на основе MAE нельзя использовать на данных прерывистого спроса.
x <- rnorm(150,30,10) * rbinom(150, 1, 0.4)
Ряд будет выглядеть примерно так:
plot.ts(x)
Пример условного ряда
Далее мы используем 100 наблюдений для построения прогнозов и 50 для сравнения их точности. Будем использовать два метода прогнозирования: простую среднюю по обучающей выборке и нулевой прогноз (который в нашем случае соответствует медиане). Они выглядят примерно так:
plot.ts(x) abline(h=mean(x[1:100]),col="blue", lwd=2) abline(h=0,col="purple", lwd=2) abline(v=100, col="red", lwd=2)
Пример условного ряда и прогнозов по двум методам: синяя линия - простая средняя, фиолетовая линия - нулевой прогноз. Красная линия делит выборку на обучающую и проверочную части
Очевидно, что средняя дала более адекватный прогноз, чем метод с нулями. По крайней мере, точечный прогноз проходит более-менее в середине ряда и на основе него можно принимать какие-то решения (например, что в среднем мы продадим около 12 единиц в день). Нулевой же прогноз не несёт никакой ценности, так как мы даже не можем сказать, стоит ли продолжать продажи продукта. Что же нам скажут наши ошибки?
errorMeasures <- matrix(c(mean(abs(x[101:150] - mean(x[1:100]))),
mean(abs(x[101:150] - 0)),
mean((x[101:150] - mean(x[1:100]))^2),
mean((x[101:150] - 0)^2)),
2,2,dimnames=list(c("Average","Zero"),c("MAE","MSE")))
errorMeasures
MAE MSE Average 15.4360 264.9922 Zero 12.3995 418.4934
Как видим, MAE рекомендует использовать нулевой прогноз (ошибка составила 12.3995 против 15.4360 в случае со средней), в то время как MSE рекомендует среднюю (264.9922 против 418.4934). Это простая иллюстрация тезиса, высказанного выше про средние и медианы.
Во-вторых, некоторые исследователи считают, что если модель оценена путём минимизации, например, MSE, то она может быть оценена только с помощью соответствующих ошибок на основе MSE. Это не совсем так. Да, скорее всего, ваша модель лучше себя покажет в том случае, если целевая функция при оценке соответствует целевой функции при тестировании модели на отдельной выборке (например, MSE и там, и там). Но это не означает, что мы не можем использовать ошибки на основе других функций. Выбор метрики должен быть мотивирован конкретными задачами (для чего мы делаем прогноз), а не тем, как мы оценивали модель. В идеале ваше конкретное управленческое решение должно быть согласовано с выбранной ошибкой. Например, при управлении запасами нам может быть важно знать, насколько модель позволяет точно сформировать страховой запас. В этом случае нам вообще могут быть нужны не ошибки на основе MAE или MSE, а более продвинутые эксперименты с симуляцией спроса.
В качестве промежуточных выводов отметим, что ошибки на основе MSE должны использоваться тогда, когда нам требуется идентифицировать метод, дающий наиболее точный средний прогноз, в то время, как ошибки на основе MAE должны использоваться для оценки медианы, вне зависимости от того, как модель была оценена.
Один из вопросов, который может возникнуть по прочтении всего этого: что же минимизируют MAPE и SMAPE? Стефан Коласса и Мартин Роланд (Stephan Kolassa and Martin Roland, 2011) показали на простом примере, что минимум MAPE достигается смещённым прогнозом, а сам Стефан в своей статье (Stephan Kolassa, 2016) обратил внимание на то, что в случае с лог нормальным распределением случайной величины MAPE минимизируется модой. Однако до сих пор совершенно непонятно, что происходит в случае с SMAPE. Это ещё одна причина, по которой SMAPE лучше не использовать (остальные обсуждались в соответствующей статье).
Мы уже знакомы с некоторыми видами ошибок, поэтому здесь мы рассмотрим только масштабированную и относительную ошибки ("scaled" и "relative" соответственно).
Масштабированные ошибки
Эти ошибки могут быть достаточно информативными при сравнении моделей. Например, sMAE и sMSE (Petropoulos & Kourentzes, 2015):
\begin{equation} \label{eq:sMAE}
\text{sMAE} = \frac{\text{MAE}}{\bar{y}},
\end{equation}
\begin{equation} \label{eq:sMSE}
\text{sMSE} = \frac{\text{MSE}}{\bar{y}^2},
\end{equation}
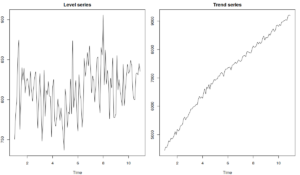
где \(\bar{y}\) - это простая средняя по обучающей выборке. У этих ошибок достаточно простая интерпретация, сходная с MAPE: они показывают средний процент отклонения по отношению к средней величине по ряду данных. Преимуществом этих ошибок является то, что они одинаково относятся к ситуациям, когда фактические значения оказались выше или ниже прогноза. Однако они привязаны к уровню ряда, поэтому в случае с нестационарными рядами могут давать противоречивые результаты. Например, в случае с рядом на графике внизу слева ошибки будут достаточно информативными, так как средняя по ряду не будет сильно меняться, однако в случае с рядом на втором графике, средняя будет меняться, поэтому и значение ошибки может изменяться только из-за этого.
Пример двух рядов данных
Rob Hyndman и Anne Koehler (2006) предложили MASE, ошибку у которой нет такой проблемы благодаря использованию первых разностей в знаменателе:
\begin{equation} \label{eq:MASE}
\text{MASE} = \frac{\text{MAE}}{\frac{1}{T-1}\sum_{t=2}^{T}|y_t -y_{t-1}|}.
\end{equation}
Идея в этом случае достаточно простая: если ряд нестационарный, можно взять его разности, которые (скорее всего) будут стационарны. Поэтому знаменатель формулы получается более-менее фиксированным, что решает обозначенную выше проблему.
К сожалению, у MASE другая проблема - её очень сложно интерпретировать. Если, например, она равна 1.3, то это ничего не значит. Да, знаменатель \eqref{eq:MASE} можно интерпретировать как среднюю абсолютную одношаговую ошибку метода Naive на обучающей выборке, но это нисколько не помогает в интерпретации. Это ошибка может использоваться для исследовательских целей, но мне сложно представить её использование на практике.
Ну, и не стоит забывать о "MAE минимизируется медианами", что в очередной раз говорит нам о том, что ни MASE, ни sMAE не следует использовать в случае с прерывистым спросом.
Относительные ошибки
Что касается относительных ошибок, то они достаточно просты в работе и интерпретации. Всё, что нужно - это посчитать MAE или RMSE, или что бы то ни было ещё нескольких методов по рядам, затем разделить эти значения для каждого ряда на ошибки метода-бенчмарка. Считаются они по следующим формулам:
\begin{equation} \label{eq:rMAE}
\text{rMAE} = \frac{\text{MAE}_a}{\text{MAE}_b},
\end{equation}
\begin{equation} \label{eq:rRMSE}
\text{rRMSE} = \frac{\text{RMSE}_a}{\text{RMSE}_b},
\end{equation}
где в числителе ошибки интересующего нас метода, а в знаменателе - ошибки бенчмарка. Зачастую в качестве метода "b" выступает метод Naive, который очень легко применить к данным. Учитывая то, что как числитель, так и знаменатель рассчитаны по одному и тому же ряду, по одной и той же его части, мы обходим проблемы с меняющимся уровнем ряда и масштабирования. К тому же, у этих ошибок простая интерпретация: если она больше 1, то наш метод оказался менее точным, чем бенчмарк, если же она меньше 1, то прогноз по нашему методу оказался точней прогноза бенчмарка. Кроме того, относительные ошибки хорошо согласуются с идеей "ценности прогноза" (Forecast Value), разработанной Майком Гиллиландом из SAS, которую можно, например, рассчитать так:
\begin{equation} \label{eq:FV}
\text{FV} = 1-\text{rMAE} \cdot 100\%.
\end{equation}
Так что, например, rMAE = 0.96 означает, что наш метод увеличивает точность прогнозов на 4% по сравнению с бенчмарком (с точки зрения MAE).
Ну, и как заметили Davydenko и Fildes (2013), если вы хотите получить агрегированную величину rMAE, то имеет смысл использовать геометрическую среднюю, а не арифметическую, так как мы имеем дело с отношением, а не с вычитанием. Кроме того, геометрическая средняя более робастна, чем арифметическая.
Главная же проблема относительных ошибок заключается в том, что если для какого-то ряда либо числитель, либо знаменатель оказывается равен нулю, то рассчитать агрегированную величину не удастся. Впрочем, это не так страшно, потому что мы всегда можем провести анализ распределения ошибок, не обязательно опираться только на одно число. К тому же, мы не часто встречаем эту проблему в реальности. Такое может наблюдаться, например, в случае с прерывистым спросом, когда в тестовой выборке сплошные нули, и Naive дал нулевой прогноз. Однако в случае с прерывистым спросом лучше не использовать Naive - он не информативен, простая средняя по ряду даст более полезную информацию. В любом случае, если вы столкнулись с подобной ситуацией, то имеет смысл просто исключить из рассмотрения ряды, в которых это произошло, потому что ситуация, в которой метод даёт прогноз с нулевой ошибкой означает, что вам ненужно строить прогноз по этому ряду.
Резюмируя всё вышенаписанное, я бы рекомендовал использовать относительные ошибки, держа в голове идею о том, что MAE минимизируется медианами, а MSE минимизируется средними. А для того, чтобы решить, что именно выбрать из этих двух, стоит задаться вопросом: что именно нам нужно измерить? В некоторых случаях может оказаться, что вам не интересны ни медиана, ни средняя, а вас интересуют квантили и верхняя граница прогнозного интервала... Но это уже совсем другая история.
Примеры в R
Для того, чтобы посмотреть, как можно работать с ошибками, мы рассмотрим простой пример с пакетом smooth v2.5.3 и несколькими рядами из базы M3.
Загрузим необходимые пакеты:
library(smooth) library(Mcomp)
Возьмём подвыборку месячных рядов демографических данных (это всего 111 рядов - должно быть достаточно для примера):
M3Subset <- subset(M3, 12, "demographic")
Создадим массив для двух ошибок: rMAE и rRMSE (они будут рассчитаны на основе функции measures() из пакета greybox). Мы попробуем применить три модели: CES, ETS с автоматическим выбором среди 30 моделей и ETS с выбором среди моделей с не мультипликативным трендом:
errorMeasures <- array(NA, c(length(M3Subset),2,3),
dimnames=list(NULL, c("rMAE","rRMSE"),
c("CES","ETS(Z,Z,Z)","ETS(Z,X,Z)")))
Проведём расчёты в цикле, записывая значения ошибок. По умолчанию, в качестве бенчмарка в rMAE и rRMSE используется метод Naive.
for(i in 1:length(M3Subset)){
errorMeasures[i,,1] <- auto.ces(M3Subset[[i]])$accuracy[c("rMAE","rRMSE")]
errorMeasures[i,,2] <- es(M3Subset[[i]])$accuracy[c("rMAE","rRMSE")]
errorMeasures[i,,3] <- es(M3Subset[[i]],"ZXZ")$accuracy[c("rMAE","rRMSE")]
cat(i); cat(", ")
}
И проанализируем результаты. Начнём с ArMAE и ArRMSE:
exp(apply(log(errorMeasures),c(2,3),mean))
CES ETS(Z,Z,Z) ETS(Z,X,Z) rMAE 0.6339194 0.8798265 0.8540869 rRMSE 0.6430326 0.8843838 0.8584140
Как видим, все модели в среднем показали себя лучше, чем Naive: ETS примерно на 12 - 16% лучше, чем Naive, а CES лучше более чем на 35%. Кроме того, CES оказалась точнее, чем оба варианта ETS как по rMAE, так и по rRMSE. Разница выглядит достаточно ощутимой. Но для более чёткого понимания ситуации, мы можем сменить бенчмарк в ошибках на ETS(Z,Z,Z):
errorMeasuresZZZ <- errorMeasures
for(i in 1:3){
errorMeasuresZZZ[,,i] <- errorMeasuresZZZ[,,i] / errorMeasures[,,"ETS(Z,Z,Z)"]
}
exp(apply(log(errorMeasuresZZZ),c(2,3),mean))
CES ETS(Z,Z,Z) ETS(Z,X,Z) rMAE 0.7205050 1 0.9707448 rRMSE 0.7270968 1 0.9706352
В этом случае мы можем сказать, что CES оказалась примерно на 28% точнее, чем ETS(Z,Z,Z). Кроме того, исключение мультипликативного тренда из рассмотрения повышает точность прогнозов примерно на 3% как для MAE, так и для RMSE.
Как я и писал ранее, мы можем не ограничиваться просто значениями, мы можем проанализировать распределение ошибок, что может дать нам дополнительную информацию о наших моделях. Самый простой вариант анализа - это боксплот:
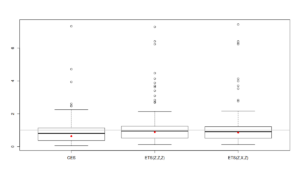
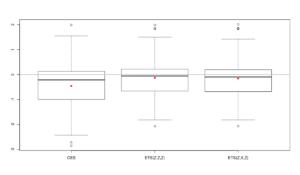
boxplot(errorMeasures[,1,]) abline(h=1, col="grey", lwd=2) points(exp(apply(log(errorMeasures[,1,]),2,mean)),col="red",pch=16)
Boxplot of rMAE for a subset of time series from the M3
Учитывая то, что распределение ошибок не симметрично, проанализировать его оказывается иногда затруднительно. Тем не менее, мы можем заметить, что ящичковая диаграмма для CES расположена ниже диаграмм других моделей, что указывает на то, что CES оказывается точнее других моделей в подавляющем числе случаев. Серая горизонтальная линия на графике соответствует единице, то есть нашему бенчмарку, Naive. Как видим, в среднем модели оказались точнее, чем бенчмарк, хотя в некоторых случаях они себя проявили хуже (части ящичков лежат над прямой линией).
В некоторых случаях боксплот в логарифмах может дать более детальную информацию:
boxplot(log(errorMeasures[,1,])) abline(h=0, col="grey", lwd=2) points(apply(log(errorMeasures[,1,]),2,mean),col="red",pch=16)
Boxplot of rMAE in logarithms for a subset of time series from the M3
Серая горизонтальная линия на графике опять соответствует Naive, но на этот раз в логарифмах (log(1)=0). В нашем случае эта диаграмма не привносит дополнительной информации, но в других случаях она может помочь в читаемости графика, так как логарифмирование может убрать влияние выбросом. Единственное, что обращает на себя внимание - это то, что первый, второй и третий квартели CES оказались ниже соответствующих квартилей ETS, но при этом есть ряд случаев, где CES оказалась менее точной (верхний ус и выбросы).
Существуют и другие методы анализа распределений, посмотрите, например, на то, как можно провести графический или статистический анализ случайных величин. Можно так же провести какой-нибудь статистический тест (например, Nemenyi), для того, чтобы выяснить, значимы ли отличия между методами статистически. Однако всё это - материалы для будущих статей.