Введение
Некоторые люди считают, что главная идея прогнозирования заключается в том, чтобы как можно более точно предсказать будущее. У меня для них плохие новости. На самом деле главная идея прогнозирования заключается в уменьшении неопределённости относительно будущего. Ведь, будущее не предопределено, мы никогда не знаем, что именно произойдёт, когда и как. Но с помощью методов прогнозирования мы можем хотя бы сказать, чего не стоит ждать и очертить область, в которой, вероятно, событие произойдёт…
В принципе, любое событие, которое мы хотим рассмотреть с точки зрения прогнозирования, может быть представлено некой систематической составляющей \(\mu_t\), которую можно описать с помощью некоторой модели, а так же случайной компонентой \(\epsilon_t\). Последняя может и не быть случайной по природе, но будет считаться случайной для целей моделирования. А всё из-за того, что мы не можем, например, предсказать, пойдёт ли конкретный человек в поликлинику в определённый день или нет. Поэтому тот спрос (или с чем вы там работаете), который мы наблюдаем в виде конкретных величин, может быть грубо описан математически следующим образом:
\begin{equation} \label{eq:demand}
y_t = \mu_t + \epsilon_t,
\end{equation}
где \(y_t\) — это фактические значения спроса (есть и другие формулы для нелинейных моделей, но они не меняют суть дискуссии, поэтому пока тут мы будем говорить о простой линейной модели). Что же мы обычно делаем в прогнозировании? Мы пытаемся как можно точнее описать систематическую составляющую \(\mu_t\), пытаясь выловить структуру и каким-то образом так же получить представление о неопределённости \(\epsilon_t\) вокруг этой структуры. Когда речь заходит об ошибке \(\epsilon_t\), мы обычно можем только что-то сказать о том, как это величина распределена, и какие у неё параметры (например, математическое ожидание и дисперсия).
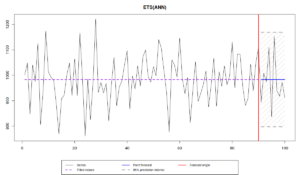
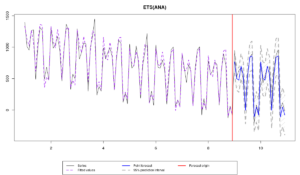
Поэтому, когда перед нами имеется какой-нибудь вот такой временной ряд:
то мы можем сказать, что средний уровень продаж составляет 1000 единиц, но так же, что вокруг этого уровня имеются некие случайные отклонения, характеризуемые каким-то СКО \(\sigma \approx 100 \). Суть прогнозирования сводится к тому, чтобы оценить как можно точнее \(\mu_t\) и \(\sigma\). Если нам удастся это сделать, то мы построим точечные прогнозы (синяя линия на графике) и прогнозный интервал шириной \(1-\alpha\) (скажем, 95-ти процентный, серая область на графике), который в идеальной ситуации будет накрывать \((1-\alpha) \times 100\)% наблюдений.
В реальности, мы никогда не знаем переменную \(\mu_t\), поэтому, в процессе построения модели мы можем либо переоценить её («underestimate», например, не включив сезонную компоненту), что приведёт к излишне высокой дисперсии и увеличенной ширине прогнозного интервала, либо недооценить её («overestimate», например, включив тренд, когда это ненужно), что приведёт к заниженной дисперсии и не реалистично узким прогнозным интервалам. Поэтому при выборе модели, мы пытаемся добраться как можно ближе к значениям \(\mu_t\) и \(\sigma\).
Когда речь заходит о непосредственном прогнозировании, мы обычно строим точечные прогнозы, которые соответствуют условной средней величине модели, призванной точно отразить будущие значения \(\mu_t\), а так же прогнозные интервалы, которые соответствуют определённым квантилям распределения и по идеи должны каким-то образом описать неопределённость случайной величины \(\epsilon_t\). На этом сайте уже была статья на тему прогнозных интервалов, а так же пару статей на тему измерения точности точечных прогнозов. В этой статье мы обсудим, как понять, правильно ли модель выловила эту самую неопределённость или нет.
Интервальный оценки
Рассмотрим следующий пример в R с использованием функций пакета smooth v2.5.4. Сгенерируем данные на основе модели ETS(A,N,A) с построим по этим данным несколько моделей:
library(smooth)
x <- sim.es("ANA", obs=120, frequency=12, persistence=c(0.3,0.1), initial=c(1000), mean=0, sd=100)
modelUnderfit <- es(x$data, "ANN", silent=F, interval=T, holdout=T, h=24)
modelOverfit <- es(x$data, "AAA", silent=F, interval=T, holdout=T, h=24)
modelCorrect <- es(x$data, "ANA", silent=F, interval=T, holdout=T, h=24)
modelTrue <- es(x, silent=F, interval=T, holdout=T, h=24)
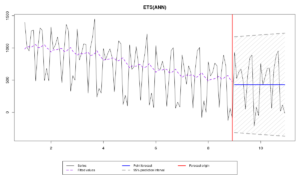
Сами данные демонстрируют меняющийся уровень ряда и изменяющуюся во времени сезонность. А четыре модели, которые мы использовали, это:
- ETS(A,N,N), которая недооценивает данные (underfitting) из-за отсутствия сезонной компоненты,
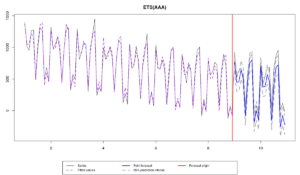
- ETS(A,A,A), которая переоценивает данные (overfitting) из-за лишней компоненты (тренд),
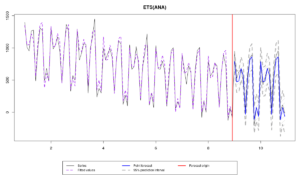
- ETS(A,N,A), которая правильно специфицирована, но параметры которой рассчитаны на основе выборки,
- ETS(A,N,A) - истинная модель, с правильными параметрами.
Все эти модели дают нам точечные прогнозы, точность которых можно оценить с помощью каких-нибудь ошибок:
errorMeasures <- rbind(modelUnderfit$accuracy,
modelOverfit$accuracy,
modelCorrect$accuracy,
modelTrue$accuracy)[,c("sMAE","sMSE","sCE")]
rownames(errorMeasures) <- c("Model Underfit","Model Overfit","Model Correct","Model True")
errorMeasures*100
sMAE sMSE sCE Model Underfit 45.134368 25.510527 -122.3740 Model Overfit 19.797382 5.026588 -449.8459 Model Correct 9.580048 1.327130 -149.7284 Model True 9.529042 1.318951 -139.8342
Обратите внимание, что в нашем примере первая модель дала наименее точный прогноз из-за отсутствия сезонной компоненты, но при этом дала наименее смещённый прогноз (sCE=-122.3740), что могло произойти просто по счастливой случайности. Вторая модель оказалась точнее первой, потому что в ней есть необходимая компонента, но не такой точной, как правильная модель из-за наличия тренда, который продолжает нисходящую траекторию на проверочной выборке. Что касается последних двух моделей, то разница в их точности достаточно мала, но, судя по всему, истинная модель оказалась немного точнее модели, оцененной по выборке.
Что более важно, все эти модели дали разные интервальные прогнозы. Проблема в том, что графически их проанализировать затруднительно. Поэтому нам стоит оценить их точность с помощью каких-нибудь показателей. Например, Mean Interval Score (MIS), предложенной Gneiting (2011) и популяризованной во время M4 Competition:
\begin{equation} \label{MIS}
\begin{matrix}
\text{MIS} = & \frac{1}{h} \sum_{j=1}^h \left( (u_{t+j} -l_{t+j}) + \frac{2}{\alpha} (l_{t+j} -y_{t+j}) \mathbb{1}(y_{t+j} < l_{t+j}) \right. \\ & \left. + \frac{2}{\alpha} (y_{t+j} -u_{t+j}) \mathbb{1}(y_{t+j} > u_{t+j}) \right) ,
\end{matrix}
\end{equation}
где \(u_{t+j}\) - это верхняя граница, \(l_{t+j}\) - это нижняя граница интервала, \(\alpha\) - это уровень значимости, а \(\mathbb{1}(\cdot)\) - это индикаторная функция, значение которой равно единице, в случае, если условие внутри неё верно, и нулю в противном случае. Идея MIS заключается в том, чтобы оценить размах интервала вместе с его охватом (сколько наблюдений было накрыто интервалом). Если фактические значения лежат вне интервала, то ошибка увеличивается пропорционально расстоянию до них с коэффициентом \(\frac{2}{\alpha}\). Кроме того, ширина интервала положительно влияет на значение индекса: чем шире интервал, тем больше значение MIS. Идеалистическая модель со значением MIS=0 должна содержать значения на границах интервал, причём \(u_{t+j}=l_{t+j}\), что означает, что будущее предопределено, никакой случайно составляющей нет. Конечно же, в реальности это просто невозможно.
Этот индекс доступен в пакете greybox для R:
c(MIS(modelUnderfit$holdout,modelUnderfit$lower,modelUnderfit$upper,level=0.95), MIS(modelOverfit$holdout,modelOverfit$lower,modelOverfit$upper,level=0.95), MIS(modelCorrect$holdout,modelCorrect$lower,modelCorrect$upper,level=0.95), MIS(modelTrue$holdout,modelTrue$lower,modelTrue$upper,level=0.95))
[1] 1541.6667 1427.7527 431.7717 504.8203
Полученные цифры сами по себе ничего нам не говорят, их надо сравнивать друг с другом. Как видим, первая модель показала себя хуже всех в плане прогнозных интервалов, в то время как правильная модель 3 настолько хороша, что даже уделала истинную модель 4 (это могло произойти по чистой случайности).
К сожалению, мы не можем сказать ничего больше по поводу интервалов на основе MIS. Поэтому для того, чтобы понять, что же именно произошло, мы можем обратиться к среднему размаху интервалов (range):
\begin{equation} \label{range}
\text{range} = \frac{1}{h} \sum_{j=1}^h (u_{t+j} -l_{t+j}) ,
\end{equation}
которая на человеческом языке означает среднюю фактической ширины интервалов с первого по h шагов вперёд. Вот как это рассчитать в R:
c(mean(modelUnderfit$upper - modelUnderfit$lower), mean(modelOverfit$upper - modelOverfit$lower), mean(modelCorrect$upper - modelCorrect$lower), mean(modelTrue$upper - modelTrue$lower))
[1] 1541.6667 297.1488 431.7717 504.8203
Глядя на эти цифры, становится понятно, что вторая модель (которая переоценивает данные) произвела самые узкие интервалы из четырёх моделей, и серьёзно недооценила неопределённость. Это привело к тому, что большая часть значений оказалась вне интервала. Заметьте так же, что ширина интервалов первой модели значительно больше ширины других интервалов. Это плохо, потому что принимать решения на их основе будет затруднительно (что-то типа "завтра мы продадим от 100 до 1600 единиц хлеба").
Что можно ещё сделать, так это рассчитать среднюю величину покрытия интервалами (coverage):
\begin{equation} \label{coverage}
\text{coverage} = \frac{1}{h} \sum_{j=1}^h \left( \mathbb{1}(y_{t+j} < l_{t+j}) \times \mathbb{1}(y_{t+j} > u_{t+j}) \right) ,
\end{equation}
что может быть сделано в R следующим образом:
c(sum((modelUnderfit$holdout > modelUnderfit$lower & modelUnderfit$holdout < modelUnderfit$upper)) / length(modelUnderfit$holdout), sum((modelOverfit$holdout > modelOverfit$lower & modelOverfit$holdout < modelOverfit$upper)) / length(modelOverfit$holdout), sum((modelCorrect$holdout > modelCorrect$lower & modelCorrect$holdout < modelCorrect$upper)) / length(modelCorrect$holdout), sum((modelTrue$holdout > modelTrue$lower & modelTrue$holdout < modelTrue$upper)) / length(modelTrue$holdout))
[1] 1.0000000 0.5416667 1.0000000 1.0000000
К сожалению, в нашем случае эта величина оказалось не очень полезной. Например, первая, третья и четвёртая модели содержат в своих интервалах 100% наблюдений, хотя должны бы содержать 95%. Что же касается второй модели, то она накрывает только 54.2% наблюдений, что, конечно же, тоже плохо. Тем не менее, глядя на размах и величину покрытия мы можем заключить, что проблема второй модели заключается в излишне узком интервале, проблема первой - в излишне широком, в то время как третья и четвёртая неплохо себя проявили в этом упражнении.
Если нам нужно получить ещё более подробную оценку точности интервалов, мы можем обратиться к пинбольной функции для каждой границы по отдельности (кажется, она была предложена Koenker & Basset, 1978):
\begin{equation} \label{pinball}
\text{pinball} = (1 -\alpha) \sum_{y_{t+j} < b_{t+j}, j=1,\dots,h } |y_{t+j} -b_{t+j}| + \alpha \sum_{y_{t+j} \geq b_{t+j} , j=1,\dots,h } |y_{t+j} -b_{t+j}|,
\end{equation}
где \(b_{t+j}\) - это значение границы интервала (верхней или нижней). Пинбол, по идеи, должен показывать, насколько точно мы оценили конкретный квантиль распределения. Чем меньше его значение, тем ближе мы оказались к квантилю. Если он равен нулю, то мы идеально попали в соответствующий квантиль.
В нашем случае, мы строили 95% прогнозный интервал, что означает, что мы целились в 2.5% и 97.5% квантили. Пинбол можно рассчитать с помощью функции пакета greybox в R:
pinballValues <- cbind(c(pinball(modelUnderfit$holdout,modelUnderfit$lower,0.025),
pinball(modelOverfit$holdout,modelOverfit$lower,0.025),
pinball(modelCorrect$holdout,modelCorrect$lower,0.025),
pinball(modelTrue$holdout,modelTrue$lower,0.025)),
c(pinball(modelUnderfit$holdout,modelUnderfit$upper,0.975),
pinball(modelOverfit$holdout,modelOverfit$upper,0.975),
pinball(modelCorrect$holdout,modelCorrect$upper,0.975),
pinball(modelTrue$holdout,modelTrue$upper,0.975)))
rownames(pinballValues) <- c("Model Underfit","Model Overfit","Model Correct","Model True")
colnames(pinballValues) <- c("lower","upper")
pinballValues
lower upper Model Underfit 484.0630 440.9371 Model Overfit 168.4098 688.2418 Model Correct 155.9144 103.1486 Model True 176.0856 126.8066
Мы вновь можем заметить, что сами по себе значения пинболов нам ни о чём не говорят - они должны сравниваться друг с другом. На основе этого сравнения можно заключить, что правильная модель 3 оказалась точнее как для 2.5%, так и для 97.5% квантилей. Она даже побила истинную модель в этом примере, что согласуется с нашими предыдущими наблюдениями. Впрочем, это пример на одном временном ряде, так что это не показательно.
Кроме того, мы видим, что первая модель оказалась хуже правильной модели в плане как верхней, так и нижней границ интервала. Это всё из-за того, что размах её интервалов оказался завышенным. Она смогла только побить вторую модель (с переоценкой) по 97.5% квантилю, а так она показала себя достаточно плохо.
Что касается второй модели, нижняя граница её интервала оказалась достаточно точной, но вот верхняя оказалась совсем никудышной. Это всё из-за тренда, который тянет прогнозы вниз.
Стоит отдельно заметить, что с пинболами работать достаточно затруднительно, так как для точной оценки квантилей требуются большие выборки. Например, для того, чтобы получить более-менее адекватное представление о том, как себя проявил 97.5% квантильный прогноз, в нашем распоряжении должно быть как минимум 40 наблюдений, чтобы 39 из них лежали ниже границы (\(\frac{39}{40} = 0.975\)). На самом деле, с квантилями вообще тяжело работать, потому что их не всегда можно точно определить. Для напоминания, математически квантиль определяется так:
\begin{equation} \label{quantile}
P \left(y_t < q_{\alpha} \right) = \alpha ,
\end{equation}
что на человеческом языке означает "вероятность того, что значение окажется ниже определённого \(\alpha\)-квантиля равна \(\alpha\)". Продолжая наш пример, если в нашем распоряжении всего лишь 20 наблюдений, мы можем хоть с какой-то точностью определить только \(\frac{19}{20} = 0.95\) квантиль. Всё, что находится между 95% и 100% в этом случае - это серая зона.
Последнее, что хотелось бы сказать по поводу всех этих индексов, это то, что они измеряются в оригинальных единицах (например, литры пива). Поэтому их нельзя агрегировать для разных временных рядов. Для того, чтобы получить правильное представление о точности интервалов, нам нужно как-то избавиться от единиц измерения. Мы можем, например, всё масштабировать с помощью средней величины (как Petropoulos & Kourentzes (2015)), либо на основе средних разностей (как Hyndman & Koehler (2006)), либо на основе относительных значений (как similar to Davydenko & Fildes (2013)).
Эксперимент в R
Для того, чтобы понять, как ведут себя все эти индексы, попробуем провести эксперимент на выборке из 1000 рядов, сгенерированных таким же образом, как и наш пример до того. Вот пример скрипта для R:
Признаюсь, это не самый эффективный код, можно было бы его распараллелить, но посчитал, что для целей нашего эксперимента, можно и подождать минут десять.
Проблема, с которой мы теперь сталкиваемся, рассчитав все эти значения по выборке из 1000 рядов - это как раз единицы измерения. Простое решение - взять одну из моделей за эталон и рассчитать относительные индексы на основе неё. В качестве такой модели я возьму правильную модель 3 (обратите внимание, что покрытие, coverage, уже измеряется в относительных величинах, поэтому его ненужно модифицировать):
errorMeasuresRelative <- errorMeasures
for(i in 1:4){
errorMeasuresRelative[,i,c(1,2,4,5)] <- errorMeasures[,i,c(1,2,4,5)] / errorMeasures[,3,c(1,2,4,5)]
}
Таким образом мы будем анализировать относительные размах, MIS и пинбол, которые можно аггрегировать как угодно, но лучше - с помощью средних геометрических:
round(cbind(exp(apply(log(errorMeasuresRelative[,,-3]),c(2,3),mean)),
apply(errorMeasuresRelative,c(2,3),mean)[,3,drop=FALSE]),3)
MIS Range Lower Upper Coverage Model Underfit 2.091 2.251 2.122 2.133 0.958 Model Overfit 1.133 1.040 1.123 1.113 0.910 Model Correct 1.000 1.000 1.000 1.000 0.938 Model True 0.962 1.013 0.964 0.963 0.951
Как видим, модель, которая недооценивает данные дала на 125.1% более широкие интервалы, чем правильная модель. У неё так же более высокие значения пинболов (на 112.2% и 113.3% выше соответственно), что означает, что она сильно промахнулась относительно 2.5% и 97.5% квантилей. Резюмируя, модель переоценила неопределённость из-за того, что в ней не оказалось необходимой сезонной компоненты. Однако, покрытие у неё оказалось очень близко к 95%, что говорит о том, что сам подход к построению интервалов оказался корректным.
Вторая модель, которая переоценила данные, обладает более широким размахом, чем правильная модель, но при этом покрывает меньше фактических наблюдений своими интервалами. В целом, хоть ситуация с этой моделью не такая критическая, как с первой, решения на основе её интервалов принимать не безопасно.
Истинная модель (последняя в таблице) произвела интервалы чуть шире, чем модель, оценённая по выборке, но при этом оказалась точнее в плане конкретных квантилей и покрыла 95.1% наблюдений, что практически неотличимо от номинального значения.
А что касается третьей модели, она оказалась лучше первых двух в плане MIS, размаха и пинбола, но при этом покрыла только 93.8% значений в выборке, что существенно ниже, чем 95%. Это всё из-за того, что мы оценивали параметры по выборке и того, как именно учитывается неопределённость в моделях ETS - подход Hyndman et al. (2008) подразумевает, что параметры известны... Это одна из неизученных проблем в области ETS на данный момент.
Вообще же, могут быть и другие причины в том, почему правильная модель дала не самые точные интервалы, некоторые из которых мы уже обсуждали в прошлом. Но главная мысль данной статьи заключается в том, что, несмотря на то, как именно мы конструируем интервалы, несмотря на то, какие модели используем и как их выбираем, у нас есть специальные инструменты, которые могут позволить нам понять, насколько правильно мы смогли уловить неопределённость.



Иван, здравствуйте.
Как всегда отличная, глубокая статья!
Здравствуйте, Андрей!
Спасибо за отзыв!
Успехов!
Иван, подскажите если точечный прогноз строится на основе стэккинга моделей (генеральная тенденция считается с помощью ETS, далее на остатках тренируется деревья решений далее прогнозы складываются) при таком методе возможно для точечного прогноза построить прогнозные интервалы?
Существуют разные методы построения прогнозных интервалов. Когда речь заходит о сложных комбинациях моделей, то параметрические и полупараметрические обычно не очень подходят. Поэтому тут можно прибегнуть к построению интервалов на основе каких-нибудь ядерных функций или что-нибудь в духе того, что обсуждалось тут: https://openforecast.org/2017/06/11/prediction-intervals/