В одной из предыдущих статей, мы обсудили, как измерить точность прогнозных методов в случае со стандартным спросом. Все эти MAE, RMSE, MASE, RMSSE, rMAE, rRMSE и прочие ошибки позволяют получить информацию о том, как методы себя проявили в среднем или в плане медианы. Мы так же обсудили, как измерять адекватность прогнозных интервалов, и должны быть знакомы с такими понятиями, как размах, покрытие, MIS и pinball. Но всё это может стать абсолютно бесполезным, если мы имеем дело с прерывистым спросом, в котором может быть много нулей и мало информации. Поэтому имеет смысл обсудить тему измерения точности прогнозов в случае прерывистого спроса. Мы уже обсудили некоторые аспекты прерывистого спроса в статье про прерывистое экспоненциальное сглаживание какое-то время назад, и мы уже рассматривали некоторые примеры прерывистых временных рядов в одной из предыдущих статей. Здесь я постараюсь предоставить немного другой взгляд на проблему.

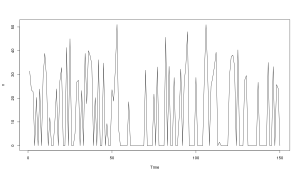
Прерывистый спрос — это спрос, который происходит не регулярно. Она означает, что в какие-то моменты времени мы будем регистрировать нули (никто не покупает продукт). Вот пример такого ряда:

Как видим, в таком ряду имеется два источника случайности: случайность в размере спроса и случайность в появлении спроса. Обратите внимание, что сам спрос не обязательно должен быть целочисленным. Речь не идёт о моделях, основанных на дискретных распределениях (таких как Пуассоновское или Отрицательное Биномиальное). Речь идёт о том, что в общем случае прерывистый спрос может быть описан формулой:
\begin{equation} \label{eq:general}
y_t = o_t z_t ,
\end{equation}
где \(y_t\) — это фактические наблюдения в момент времени \(t\), \(o_t\) — это бинарная переменная появления спроса, а \(z_t\) — это размер спроса. В то время как некоторые статистические модели не делают такого разделения, наиболее популярные методы прогнозирования основаны либо прямо либо косвенно на этой формуле.

Хоть в теории мы можем построить какую-нибудь сложную модель (например, на основе нейронных сетей), обычно мы не можем точно спрогнозировать, когда именно продукт купят и в каком количестве. У нас скорее есть возможность сказать, сколько купят в среднем (точечный прогноз) или сколько купят в 95% случаев (прогнозный интервал). Но даже если мы построим такие прогнозы, следующий вопрос будет: «И что же с этим делать?»

В случае с цепями поставок, типичное решение — это сколько заказать или произвести единиц продукции, учитывая то количество, которое уже у нас есть, спрос на продукт, который мы наблюдаем, и скорость доставки необходимого сырья / продукции контрагентами. В этом случае речь чаще всего идёт о величине страховых запасов — сколько единиц продукции нам нужно иметь на складе, чтобы удовлетворить спрос до тех пор, пока не доставят новую партию, да ещё так, чтобы полки в магазине не пустовали. Обычно эта величина рассчитывается как квантиль какого-нибудь распределения. Во многих случаях, на практике для этого используется Нормальное распределение, что, конечно же, в нашем случае совершенно не верно по многим причинам (начнём хотя бы с того, что оно предполагает, что спрос может быть отрицательным). Но не будем вдаваться в детали по этому поводу, попробуем понять, что такой процесс нам даёт в плане оценки точности прогнозов.

Страховые запасы обычно определяются исходя из времени на выполнение заказа (lead time). Например, если мы знаем, что следующую партию продукции нам привезут не раньше, чем через 2 недели, то нужно иметь такое количество продукции на складе, которое смогло бы удовлетворить спрос в течение этих двух недель, и не в среднем, а, скажем, в 95% или в 99% случаев (в зависимости от того, что решит компания). Как же получить величину страхового запаса? Тут как раз на сцену выходит наша прогнозная модель. Но фактически все рассуждения про страховой запас говорят нам о том, что нам нужен не просто точечный прогноз на каждый день, а скорее агрегированный за тот самый период доставки (например, две недели). Это первое важное отличие прогнозирования для управления запасами от прогнозирования для других целей (например, статья Kourentzes et al., 2019 обсуждает похожую проблему).

Как видим, связь между фактическим наблюдаемым спросом и финальным решением о том, сколько нужно заказать, непростая. Это так же означает, что и все те прекрасные прогнозные ошибки, которые мы обсуждали в предыдущих статьях, могут и не дать нам необходимой информации о том, как именно модели себя ведут в этой ситуации. Модель может дать очень точный прогноз, но это не обязательно означает, что он будет автоматически транслироваться в более точный заказ для конкретной ситуации. Если в таких условиях нужно оценить точность прогнозной модели, то имеет смысл работать с кумулятивными значениями (за промежуток времени на выполнение заказа), а не просто наблюдаемыми в каждый момент времени. Математически это означает работу с:
\begin{equation} \label{eq:demandOverTheLeadTime}
Y_{t+h} = \sum_{j=1}^h {y}_{t+j} ,
\end{equation}
где \(h\) — это время на выполнение заказа. На основе этого мы можем измерить среднюю точность модели, чтобы понять, как та себя ведёт в плане рабочих запасов. В случае с аддитивной моделью это сводится к расчёту:
\begin{equation}
\begin{aligned}
\text{E} \left(\sum_{j=1}^h {y}_{t+j} \right) = & \text{E}\left(\sum_{j=1}^h (\hat{y}_{t+j}+e_{t+j})\right) = \\
& \sum_{j=1}^h \text{E}(\hat{y}_{t+j}) + \sum_{j=1}^h \text{E}(e_{t+j}) = \sum_{j=1}^h \text{E}(\hat{y}_{t+j}).
\end{aligned} \label{eq:workingStock}
\end{equation}
где \(\hat{y}_{t+j}\) — это точечный прогноз, сгенерированный моделью. В данном случае это значит, что мы можем дать точечный прогноз на \(h\) шагов вперёд и просто агрегировать его и сравнить с фактическими значениями \eqref{eq:demandOverTheLeadTime} за тот же период. Однако, если мы имеем дело с аддитивными моделями, то мы фактически подразумеваем, что спрос может быть и отрицательным, что во многих случаях имеет очень далёкое отношение к реальности, особенно в случае с прерывистым спросом. В таком случае нужна другая модель (например, с мультипликативными ошибками), а это означает, что формула \eqref{eq:workingStock} может быть и не применима. В таком случае, мы вынуждены прибегать к симуляциям: генерировать множество возможные траектории будущих значений, суммировать каждую из них, и затем рассчитывать среднюю.

Предположим, что мы смогли сгенерировать кумулятивный точечный прогноз. Как теперь оценить его точность? В этом случае мы можем использовать ошибки на основе RMSE (как мы уже обсуждали в одной из предыдущих статей), так как они минимизируются средними значениями. Для оценки точности модели в плане рабочих запасов можно воспользоваться формулой квадратической кумулятивной ошибки (Squared Cumulative Error):
\begin{equation} \label{eq:workingStockRMSCE}
\text{SCE} = \left( \sum_{j=1}^h y_{t+j} -\sum_{j=1}^h \hat{y}_{t+j} \right)^2 .
\end{equation}
На основе неё можно рассчитать относительные или масштабированные ошибки, если нужно оценить точность моделей по выборке временных рядов. Всё, что мы обсуждали в статье про точность прогнозов применимо и в этом случае, если мы используем кумулятивные значения и ошибки на основе RMSE. Одна из проблем, которая может возникнуть при расчёте относительных ошибок — это использования метода Naive в качестве бенчмарка. На практике бывают ситуации, когда проверочная часть выборки содержит нули, и Naive прогнозирует, что будут нули просто по счастливому стечению обстоятельств. В таком случае мы получим деление на нуль, что сделает такую прогнозную ошибку как rRMSE бесполезной. Простое решение данной проблемы — использование средней по всему ряду вместо Naive.

Помимо стандартных прогнозных ошибок, есть и ориентированные на запасы, близкие по своей идее к SCE. Одна из таких называется «Периоды-в-Запасе» («Periods-In-Stock» — PIS, Walstrom, 2010):
\begin{equation} \label{eq:workingStockPIS}
\text{PIS} = \sum_{j=1}^h \hat{y}_{t+j} -\sum_{j=1}^h y_{t+j} .
\end{equation}
Вы обратили внимание на то, что в ней идёт вычитание фактических значений из прогнозных, а не наоборот, как обычно принято в литературе по прогнозированию? Это сделано не просто так. Авторы специально поменяли местами эти составляющие, для того, чтобы PIS была ближе по смыслу к конкретным решениям в управлении запасами. Так, отрицательное значение PIS будет говорить об упущенных продажах, в то время как положительное будет указывать на избыточные запасы. Что нужно иметь в виду, так это то, что по тем же причинам, по которым агрегирование MAE или RMSE для разных продуктов не имеет смысл, мы не можем агрегировать PIS для яблок и груш. Petropoulos & Kourentzes (2015) предложили несколько модификаций для PIS, которые позволяют решать эту проблему.

Хорошо, мы разобрались более-менее с рабочими запасами. Однако хорошая точность в плане рабочих запасов не означает хорошую точность в плане страховых запасов. Поэтому надо разобраться, как оценивать точность во втором случае. Ближайшее, что мы можем получить для оценки страховых запасов — это оценка точности конкретного квантиля агрегированного (во времени) распределения. До нижней границы интервала в управлении запасами нам обычно нет дела, нам интересна верхняя. Поэтому в реальности нам нужно провести симуляции, используя модель (что-нибудь типа 1000 итераций различных вариантов развития событий), агрегировать каждую из полученных траекторий, после чего взять конкретный квантиль, соответствующий желаемому уровню страховых запасов (например, 95%). В некоторых конкретных случаях мы можем и не прибегать к симуляциям, но в таких случаях наши предположения могут сильно отличаться от реальности (например, нормальность распределения ошибок).

Ну, предположим, что мы рассчитали значение для нужного квантиля. Что дальше? Я бы рекомендовал использовать пинбольную функцию, не забывая о её преимуществах и недостатках. Мы так же можем рассчитать размах, покрытие и, если нам очень нужно что-то типа MIS, мы можем обратиться к квантильной величине («Quantile Score» — QS, Gneiting, 2007), потому что мы имеем дело с одной границей, а не со стандартным интервалом:
\begin{equation} \label{QS}
\text{QS} = \left(Y_{t+h} — U_{t+h} \right) \left(\mathbb{1} \left\{ Y_{t+h} \leq U_{t+h} \right\} -\alpha \right) ,
\end{equation}
где \(\alpha\) — это доверительная вероятность (например, 95% или 99%), \(U_{t+h}\) — это значение квантиля, а \(\mathbb{1}(\cdot)\) — это индикаторная функция, которая равна единице, если значение внутри верно и ноль в противоположной ситуации. Интерпретация QS аналогична интерпретации MIS: если фактическое значение лежит ниже границы, тогда финальное значение пенализируется меньше, чем в случае, если оно лежит выше (это определяется индикаторной функцией). QS всегда будет положительной и равной нулю только в утопической ситуации, когда все значения лежат прямо на границе \(U_{t+h}\). Главное различие между pinball и QS заключается в том, что первый пытается оценить, насколько точно измерен конкретный квантиль, а вторая пытается оценить одновременно размах и покрытие интервала. С этих позиций можно заключить, что QS несколько ближе к тому, что нас интересует в реальной жизни: мы хотим выбрать такой страховой запас, чтобы покрытие было близко к номинальному уровню (чтобы мы достигли номинального сервисного уровня), но при этом с наименьшим возможным размахом (чтобы мы не несли затраты на содержание излишков продукции). На основе QS можно рассчитать всё те же относительные или масштабированные ошибки, чтобы оценить, как модели себя показали на разных продуктах.

Ну, хорошо, более-менее разобрались с управлением запасами. А как там насчёт других областей, в которых встречается прерывистый спрос? В некоторых из них ситуация будет похожа на описанную выше, просто термины и конкретные решения будут немного другими. Но в других случаях, нас могут интересовать более классические вопросы. Например, в случае прогнозирования числа пациентов в госпитале, нам не нужны аккумулированные значения, так что мы можем работать с тем, сколько человек придёт в каждый конкретный час в следующие 12 часов. При этом среднее число пациентов может быть не таким полезным, как число в 95% и в 5% случаев, то есть в таком случае мы обращаемся к классическому прогнозному интервалу. Эти интервалы затем могут использоваться при принятии решений о том, сколько докторов и медсестёр должно быть в госпитале в ближайшие 12 часов, какое количество медикаментов должно быть в распоряжении и т.п. Обратите внимание, что сам прогнозный интервал не связан с конкретным решением (сколько шприцов иметь), но он может считаться своеобразным приближением к нему, если мы знаем, каким должно быть типичное количество персонала для конкретного числа пациентов. Ну, и, конечно же, это означает, что нам надо оценивать точность прогнозных интервалов, а не точечных прогнозов. Применительно к прерывистому спросу мы, возможно, опять столкнёмся с ситуацией, когда нам важнее понять, насколько точна верхняя граница интервала, так как нижняя будет, скорее всего, соответствовать нулю. Соответственно использование QS в этом контексте так же может иметь больший смысл, чем MIS.

Закончить эту несколько сумбурную статью хочется неожиданной рекомендацией: избегайте прерывистый спрос любой ценой. Прежде чем бросаться в моделирование с головой, подумайте, какие именно решения вы принимаете на основе прогнозов. Возможно, вам не нужны прогнозы на уровне дневных данных, так как все решения принимаются на недельном уровне (каждый понедельник мы решаем, сколько продукции заказать на неделю вперёд), и, если вы перейдёте к недельным данным, то никакой прерывистости уже не будет. А, возможно, никакого прогнозирования в вашей конкретной ситуации и не надо делать, просто потому что решения принимаются совершенно иначе на основе совсем других соображений. В любом случае, прежде чем бросаться в тёмный омут, подумайте на тему того, какие именно и как именно решения принимаются в вашей компании.