В одном из последних исследований мне потребовалось сгенерировать много временных рядов, используя модель экспоненциального сглаживания (ETS). В какой-нибудь будущей статье на сайте я обязательно подробней расскажу об этой модели, сейчас же главная мысль — это то, что с помощью неё можно генерировать сезонные / не сезонные данные, а так же с трендом / без тренда. Наличие или отсутствие этих компонент обычно отражается в названии модели. Например, ETS(M,A,N) говорит о том, что в модели мультипликативная ошибка («M» на первой позиции), аддитивный тренд («A» на второй позиции) и нет сезонности («N» на третьей позиции). Не вдаваясь в детали, компоненты могут отсутствовать («N»), быть аддитивными («A») или мультипликативными («M»).

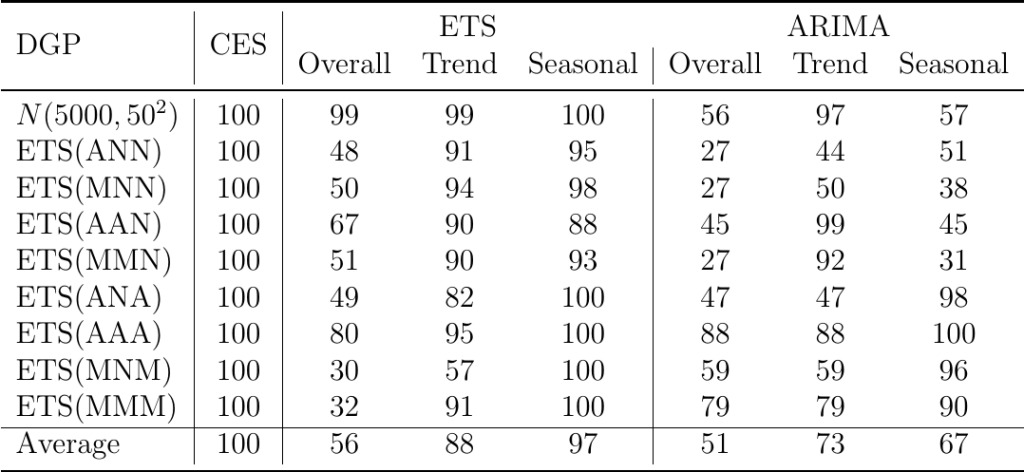
Так вот, к чему я это всё? В рамках эксперимента для упомянутой выше статьи я сгенерировал по сто месячных временных рядов, размером в 120 наблюдений для каждого из процессов представленных в таблице ниже в столбце «DGP»:

DGP — это «Data Generating Process» — название процесса, с помощью которого данные и генерировались. Помимо ETS, сто рядов данных были сгенерированы из нормального распределения (\( N(5000,50^2) \)). То есть это ряды данных без тренда, без сезонности, с постоянным математическим ожиданием и дисперсией.

Итак, в таблице представлены проценты правильной идентификации компонент ряда тремя моделями: «CES», «ETS» и «ARIMA». «Overall» для ETS — это количество случаев, когда модель, построенная по уже сгенерированным временным рядам, сумела идентифицировать компоненты, которые использовались при создании ряда. «Trend» для ETS — это количество случаев, в которых модель правильно идентифицировала тренд, а «Seasonal» — соответственно сезонность.

Для ARIMA ситуация была посложней: «Seasonal» обозначает число случаев, в которых модель сумела удачно определить, с сезонным или не сезонным рядом она имеет дело (наличие любых сезонных элементов: SAR, SMA или сезонные разности — рассматривалось как идентификация сезонности). В столбце «Trend» приведены количества случаев, когда ARIMA, построенная по рядам данных, правильно идентифицировала тренд в каком-нибудь виде (критерии: наличие дрейфа / вторые разности / первые разности + AR(p) элемент). «Overall» для ARIMA — это процент случаев, когда и тренда, и сезонность были правильно идентифицированы.

У CES ситуация простая: она определяет наличие или отсутствие тренда автоматически, поэтому остаётся только выбрать есть или нет сезонности в данных. Делается это автоматически с помощью функции ces.auto в R.

Итак, если взглянуть на таблицу, увидим любопытные результаты.

Для начала взглянем на ETS. Теоретически она должна была точно идентифицировать подавляющее число рядов, однако это произошло не везде.

1. ETS хуже всего справилась с идентификацией рядов с мультипликативной ошибкой.
2. ETS не очень хорошо справилась с идентификацией трендов в рядах, сгенерированных по модели ETS(M,N,M). В остальных случаях, однако, тренды были идентифицирован в основном правильно.
3. ETS умудрилась идентифицировать сезонность в 12% случаев в несезонных рядах, сгенерированных с помощью ETS(A,A,N).

Построение ETS происходило с помощью соответствующей функции в R («ets» пакета «forecast»). Вывод, который следует из этого — реализованный подход к определению компонент не идеален. Тем не менее он работает достаточно эффективно в подавляющем числе случаев.

Теперь ARIMA.

1. ARIMA решила, что сезонность есть в половине (а иногда и большем числе) случаев несезонных рядов данных (первые пять типов рядов). То есть она уловила то, что в этих рядах просто отсутствует по определению! Фактически это означает, что она приняла случайность за закономерность в 50% случаев.
2. Так же практически в 50% случаев ARIMA воспроизвела тренд в тех рядах данных, в которых тренда не было (ряд №2, 3, 6, 8). Здесь, правда, стоит сделать ремарку: определение тренда в ARIMA отличается от ETS, поэтому такие результаты для неё простительны.
3. Хуже всего в графе «Overall» ARIMA себя проявила в рядах №2, 3 и 5. В основном это вызвано неправильной идентификацией сезонности, но этим оно не ограничивается.

Заметим, в данном эксперименте использовалась функция Роба Хайндмана «auto.arima» из пакета «forecast». Теоретически можно было бы все претензии с неправильной идентификацией высказать автору этой функции, но изучение коррелограмм, последовавшее за этим экспериментом, указывает на то, что функция всё сделала правильно: следуя методологии Бокса-Дженкинса, мы точно так же должны были бы включить сезонные компоненты в несезонных рядах данных из-за наличия статистически значимых коэффициентов автокорреляции на лагах, кратных 12.

Выводы делайте сами.