Неминуемо на этом сайте в какой-то момент вы столкнётесь с комплексными числами. Поэтому я решил немного рассказать о них.

Но для начала краткая история появления чисел.

Краткая история появления чисел

В одной старой заброшенной пещере жило племя «Ку» доисторических людей. Жило оно так же как все: носило одежду из шкур и листьев, питалось красными да синими ягодами, и все объекты в мире воспринимало в форме «один» и «не один». Вот и в их племени было «не один» человек. Так бы и жили они дальше и ни о чём не задумывались, питались бы ягодами, да не знали бед, если бы однажды Уга, жена Учу, вождя племени, не обнаружила в лесу волшебные плоды. Были они красные, сочные, вкусны и размером с кулак, поэтому унести она могла немного. Уга была умной доисторической женщиной, поэтому она решила, что этих плодов нужно взять ровно столько, сколько доисторических людей жило в племени. Впрочем, «не один» плохо описывало нужное количество, поэтому она задумала что-то страшное — взять и придумать такие штуки, которые характеризовали бы количество людей в племени. Так Уга фактически изобрела множество натуральных чисел. Имея его, она уже могла взять ровно девять плодов и ни плодом больше.

Прошли годы, Уга постарела, ей исполнилось 26 лет, но она продолжала ходить в лес за плодами и по старой привычке приносила девять штук. Однако однажды вождь, видя девять плодов, рассердился. Он сказал ей:

«Уга уга у а учу ачу!»

И тогда Уга поняла свою ошибку. Дело в том, что этим утром к ним пришёл сосед из племени «Ук», которого Учу хотел съесть на ужин, и для того, чтобы сделать это он решил предварительно накормить и усыпить гостя. Поэтому ему нужно было десять плодов, а не девять, как обычно. А недальновидная Уга как обычно… Не долго думаю, Уга сообразила, что не хватает ещё одного плода, открыв таким образом отрицательные числа. Объединив в своём воображении множество натуральных чисел, отрицательные числа и ещё странное число «нуль», которое характеризовало число плодов, доставшееся в результате всего этого ей лично, Уга пришла ко множеству целых чисел.

Шли годы. Уга взрослела. Ей исполнилось 27. Она уже вышла на пенсию и перестала быть любимой женой Учу. За плодами ходили уже более сильные женщины, а ей просто доставалось то, что доставалось. Очень часто она получала ни один целый, большой, вкусный и сочный плод, а половину или того меньше маленького, кислого, зелёного и сморщенного. Слава богу ягоды всегда оставались целыми — их разделить на части в условиях доисторического хозяйства было невозможно. Именно в этот период своей жизни, получая половины, четверти, одни девятые и десятые, она открыла для себя дробные числа. Объединив дробные числа с множеством целых, соблюдая свой рацион из целых ягод и дробных плодов, она получила множество рациональных чисел.

Долго ли, коротко ли, но в один осенний день, когда Уга рассчитывала сторону гипотенузы по теореме Пифагора, она столкнулась со странным числом. Каждый из катетов треугольника был равен одному локтю, а вот гипотенуза получалась равной корню квадратному из двух квадратных локтей. Число \( \sqrt{2} \) было для неё странным и непонятным. Она чувствовала, что такое число было примерно равно 1.41421356237, но никак доказать этого не могла. Более того, она понимала, что это число находится где-то между 1.41421356236 и 1.41421356238, но при этом не по середине, а как-то иначе. В общем, во множестве рациональных чисел такому числу места не было. И, конечно же, Уга отдавала себе отчёт в том, что испытывает определённые затруднения при попытке связать это число с реальным миром. Потом она обнаружила и другие странные числа, такие как \( \sqrt{3} \), \( \ln(2) \), \( \pi \) и \( e \) (число Эйлера). В связи с тем, что таких чисел набиралось уже много, но толкового объяснения им дать не получалось, Уга назвала множество таких чисел иррациональным и расслабилась. Не будучи глупой женщиной (особенно для древних людей), она не растерялась и объединила множества рациональных и иррациональных чисел во множество действительных чисел, решив, что она может совершать с ними любые действия, какие захочет.

Но одной зимой, когда Уга шила одежду из шерстяной ткани она столкнулась с нестандартной ситуацией. Для того, чтобы доделать вечернее платье, ей не хватало четырёх квадратных метров серой шерстяной ткани. Вспоминая пример с плодами из своей молодости, она, будучи развитым и абстрактно мыслящим существом, решила, что у неё в распоряжении -4 квадратных метра ткани. Ну, так ей было легче понимать и воспринимать, а так же общаться с соплеменниками, кто мы такие, чтобы её за это корить? Когда же её помощница Агу спросила, какой длины ей нужна ткань, она недолго думая извлекла корень квадратный из недостающей площади и вышла в астрал. Дело в том, что операция, которую она выполнила, не работала в области действительных чисел. Посудите сами: \( \sqrt{-4} = 2 \sqrt{-1} \), но в области действительных чисел такого числа не было (прям как ситуация со рациональными и иррациональными числами). Тогда она, посчитав, что только воображает эту длину ткани, решила такие числа называть воображаемыми или мнимыми, а число \( \sqrt{-1} \) обозначила латинской буквой «i» и назвала мнимой единицей. Так на свет появилось множество мнимых чисел. Не долго думая, Уга объединила множества действительных и мнимых чисел, получив множество комплексных чисел, замкнутое относительно любых математических операций. Последняя фраза значила, что чтобы она ни делала с числами в этом множестве, а парадоксов она больше не встречала.

Конечно же, всё это забылось после того, как Угу сгрыз саблезубый бобёр, и человечеству пришлось пройти по пути всех этих математических открытий ещё раз, но мне об этой истории доподлинно известно из своего воображения!

Кстати, Гаусс не разделял идеи Уги о названиях множеств. Он говорил, что, если бы числа 1, -1 и \( \sqrt{-1} \) назывались «прямой», «обратной» и «побочной», а не «положительной», «отрицательной» и «мнимой» единицами, то никакой мистики вокруг этих чисел не было бы. Посудите сами, то, что число «отрицательное» ещё не говорит о том, что оно плохое (как отрицательный персонаж), «иррациональное» — не говорит о том, что оно не разумно, а «мнимое» — не говорит о том, что оно не существует (якобы в отличие от всех остальных «действительных» чисел). Так что Уга с названиями поторопилась… Но что возьмёшь с доисторического человека?!

Что такое комплексное число

Итак, комплексное число — это число, состоящее из двух частей: действительной и мнимой. Записывается оно обычно в виде:

\begin{equation} \label{eq:algebraic}
z = a + bi ,
\end{equation}

где a и b — действительные числа, i — мнимая единица, число удовлетворяющее равенству \( i^2 = -1 \).

Действительная часть комплексного числа иногда обозначается следующим образом: \( a = Re(z) \), — в то время как мнимая обозначается так: \( b = Im(z) \).

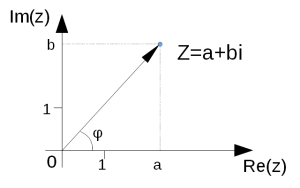
Типичное комплексное число можно представить как вектор на плоскости следующим образом:

Как и любой вектор комплексное число может характеризоваться помимо координат ещё и углом наклона \( \varphi \) (он же «полярный угол» и «аргумент») и длиной (которая так же известна под именем «модуль»). Для сравнения любое действительное число может быть представлено как точка на прямой, либо вектор, проложенный вдоль прямой, например вот так:

То есть переход от действительных к комплексным числам — это фактически переход от прямой к плоскости. Этакое расширение сознания…

Угол наклона комплексного числа может быть найден на основе знаний из курса геометрии, например, следующим образом:

\begin{equation} \label{eq:angle}
\varphi = arg(z) = arctan \left( \frac{b}{a} \right) + 2 \pi k, k \in Z
\end{equation}

Иногда для упрощения допускают, что \( k = 0\), выкидывая таким образом множество ненужных углов.

Следую теореме Пифагора, длина вектора находится по следующей формуле:

\begin{equation} \label{eq:magnitude}
R = \sqrt{a^2 + b^2}
\end{equation}

Используя всю ту же геометрию, каждую из частей в \eqref{eq:algebraic} можно представить через косинус и синус полярного угла следующим образом:

\begin{equation} \label{eq:trigonometric}
z = a + bi = R cos \varphi + i R sin \varphi = R \left( cos \varphi + i sin \varphi \right),
\end{equation}

Но на этом формы представления комплексных чисел не заканчиваются. Один товарищ по имени Эйлер после того как вывел своё число предложил следующее представление комплексного числа:

\begin{equation} \label{eq:exponential}
z = R e^ {i \varphi},
\end{equation}

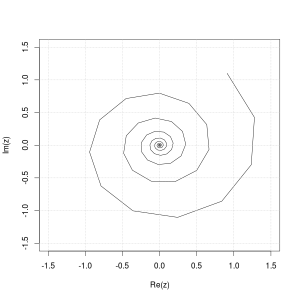
Такая форма представления называется экспоненциальной и она очень удобна при перемножении комплексных чисел — всё, что нужно сделать в таком случае это перемножить модули и сложить полярные углы. Как следует из этого описания при умножении одного комплексного числа на другое происходит изменение длины и полярного угла первого. Это приводит к его «вращению» вокруг начала координат и либо увеличению, либо уменьшению модуля. В итоге можно получать такие красивые, но не всегда полезные графики на комплексной плоскости:

С комплексными числами можно без зазрений совести проводить операции сложения, вычитания, умножения, деления, возведения в любую степень, логарифмирования и вообще чего угодно. Можно даже решать уравнения типа \(cos \varphi = 2 \)! В результате этих операций всегда будет получаться число, входящее во множество комплексных чисел. Единственное, чего нельзя делать — это делить на ноль, но об этом даже дети знают!