Авторы: Ivan Svetunkov, Nikolaos Kourentzes, Keith Ord.
Журнал: Naval Research Logistics
Аннотация на английском: Exponential smoothing has been one of the most popular forecasting methods used to support various decisions in organisations, in activities such as inventory management, scheduling, revenue management and other areas. Although its relative simplicity and transparency have made it very attractive for research and practice, identifying the underlying trend remains challenging with significant impact on the resulting accuracy. This has resulted in the development of various modifications of trend models, introducing a model selection problem. With the aim of addressing this problem, we propose the Complex Exponential Smoothing (CES), based on the theory of functions of complex variables. The basic CES approach involves only two parameters and does not require a model selection procedure. Despite these simplifications, CES proves to be competitive with, or even superior to existing methods. We show that CES has several advantages over conventional exponential smoothing models: it can model and forecast both stationary and non-stationary processes, and CES can capture both level and trend cases, as defined in the conventional exponential smoothing classification. CES is evaluated on several forecasting competition datasets, demonstrating better performance than established benchmarks. We conclude that CES has desirable features for time series modelling and opens new promising avenues for research.
Ссылка на черновую версию статьи.
DOI: 10.1002/nav.22074
Идея Комплексного Экспоненциального Сглаживания
Одна из фундаментальных идей в прогнозировании — это декомпозиция временного ряда на несколько ненаблюдаемых компонент (описание этого процесса есть, например, «>в моей монографии). Обычно говорят, что временной ряд содержит компоненты уровня, тренда, сезонности, а так же ошибку. Это популярное разбиение на компоненты и используется, например, при построении ETS, внутри которой выбор подходящих компонент осуществляется на основе информационных критериев. Однако, не у всех временных рядов есть такое чёткое разделение на компоненты, да и само разделение можно считать условным. Например, ряд со слабым трендом на практике может быть не отличим от ряда с быстро меняющимся уровнем. Кроме того, в реальности всё немного сложнее, чем нам кажется и взаимодействие компонент может быть нелинейным.
Комплексное Экспоненциальное Сглаживание (КЭС) моделирует нелинейность во временных рядах и позволяет описывать структуру ряда по-другому. Вот как выглядит модель КЭС математически:
\begin{equation} \label{eq:cesalgebraic}
\hat{y}_{t} + i \hat{e}_{t} = (\alpha_0 + i\alpha_1)(y_{t-1} + i e_{t-1}) + (1 — \alpha_0 + i — i\alpha_1)(\hat{y}_{t-1} + i \hat{e}_{t-1}) ,
\end{equation}
где \(y_t\) — это фактическое значение, \(e_t\) — это ошибка прогноза, \(\hat{y}_t\) — прогнозируемое значение на шаг вперёд, \(\hat{e}_t\) — это прокси прошлых ошибок, \(\alpha_0\) и \(\alpha_1\) — это постоянные сглаживания, а \(i\) — это мнимая единица, число удовлетворяющее уравнению \(i^2=-1\). Из-за использования комплексных переменных, модель позволяет распределять веса во времени нелинейным образом. Это становится более понятно, если в правую часть уравнения \eqref{eq:cesalgebraic} включить само же уравнение, затем повторить это и получить:
\begin{equation} \label{eq:cesalgebraicExpanded}
\begin{aligned}
\hat{y}_{t} + i \hat{e}_{t} = & (\alpha_0 + i\alpha_1)(y_{t-1} + i e_{t-1}) + \\
& (\alpha_0 + i\alpha_1) (1 — \alpha_0 + i — i\alpha_1) (y_{t-2} + i e_{t-2}) + \\
& (\alpha_0 + i\alpha_1) (1 — \alpha_0 + i — i\alpha_1)^2 (y_{t-3} + i e_{t-3}) + \\
& … + \\
& (\alpha_0 + i\alpha_1) (1 — \alpha_0 + i — i\alpha_1)^{t-2} (y_{1} + i e_{1}) + \\
& (1 — \alpha_0 + i — i\alpha_1)^{t-1} (\hat{y}_{1} + i \hat{e}_{1}) .
\end{aligned}
\end{equation}
Возведение комплексного числа \((1 — \alpha_0 + i — i\alpha_1)\) в степень в формуле выше позволяет распределять веса между наблюдениями нелинейным образом. Графически это может быть представлено следующим образом (синяя линия — веса для фактических значений, зелёная — для прогнозных ошибок):
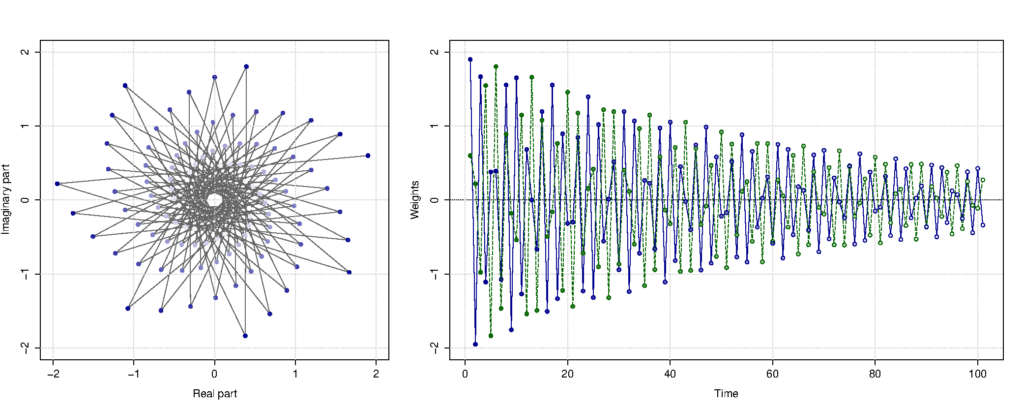
Распределение весов между наблюдениями на комплексной и действительной плоскостях. Синяя линия — веса для фактических значений, зелёная — для прогнозных ошибок.
В зависимости от значение комплексной постоянной сглаживания \(\alpha_0 + i\alpha_1\), распределение весов будет иметь разный вид. Но оно не обязательно должно быть гармоническим как на рисунке выше, оно может и убывать по классической экспоненте (как у простого экспоненциального сглаживания ака метода Брауна). Именно это гибкое распределение весов даёт КЭС особенную гибкость и позволяет ему быть эффективно применимым как к стационарным, так и нестационарным данным без переключения между компонентами временного ряда.
В опубликованной статье, мы также обсуждаем сезонную модификацию КЭС, которая позволяет моделировать как аддитивную, так и мультипликативную сезонность. Я не привожу формулы и детальное объяснение в данной статье, рекомендую всех заинтересованных обратиться к первоисточнику.
Пример в R
В R, КЭС реализовано в функции ces() пакета smooth. В том же пакете есть функция auto.ces(), позволяющая автоматически выбирать между не сезонными и сезонными моделями КЭС на основе информационных критериев. Синтакс функций похож на синтекс es() и adam(). Вот пример применения функции:
cesModel <- smooth::auto.ces(BJsales, holdout=TRUE, h=12) cesModel
Time elapsed: 0.05 seconds
Model estimated: CES(n)
a0 + ia1: 1.9981+1.0034i
Initial values were produced using backcasting.
Loss function type: likelihood; Loss function value: 249.4613
Error standard deviation: 1.4914
Sample size: 138
Number of estimated parameters: 3
Number of degrees of freedom: 135
Information criteria:
AIC AICc BIC BICc
504.9227 505.1018 513.7045 514.1457
Forecast errors:
MPE: 0%; sCE: 0.7%; Asymmetry: -5%; MAPE: 0.4%
MASE: 0.857; sMAE: 0.4%; sMSE: 0%; rMAE: 0.329; rRMSE: 0.338
Описание выше уже как-то обсуждалось в одном из прошлых постов на примере функции es(). Главное отличие между тем, что возвращают функции es() и ces() - это параметры. В данном случае, мы видим, что комплексная постоянная сглаживания \(\alpha_0 + i\alpha_1 = 1.9981 + i 1.0034\). Полученную модель можно использовать в прогнозировании, например, так:
cesModel |> forecast(h=12, interval="p") |> plot()
что даст такой график:
Сама функция ces() не изменилась с момента окончания мною PhD в 2016 году, так что результаты, например, вот этого сравнения всё ещё актуальны. Модель не обязательно даёт самые точные прогнозы во всех случаях, но как, например, было показано в статье Petropoulos & Svetunkov (2020), она привносит в комбинации то, чего не привносят другие модели. Всё из-за того, что КЭС позволяет хорошо вылавливать долгосрочные тенденции во временных рядах.
Послесловие
В качестве послесловия, я хотел бы выразить свои благодарности нескольким людям. Во-первых, это Никос Курентзес, который поверил в мою модель в далёком 2012 году и поддерживал меня все эти годы без колебаний. Во-вторых, это Кит Орд, который помог мне в некоторых выкладках и затем оказал серьёзную поддержку статье и помог придать ей ту форму, которая она имеет в конце концов. Ну, и, конечно же, я благодарен своему папе, Сергею Геннадьевичу Светунькову, который направлял меня в моей исследовательской деятельности в самом её начале и верил в меня и мои исследования ещё тогда, когда никто о них ничего не подозревал.
Если вы хотите узнать больше про модель, вам придётся прочитать статью на английском (она также доступна онлайн на сайте издателя) или же прочитать на английском историю статьи.




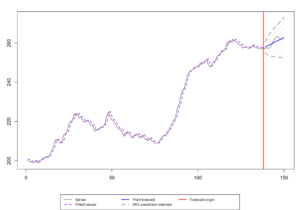
Или я дальтоник, или зелёный цвет на рисунке очень слабый. Рекомендую автору заменить его на красный цвет, тогда всё будет видно