Previously we discussed how to measure accuracy of point forecasts and performance of prediction intervals in different cases. Now we look into the question how to tell the difference between competing forecasting approaches. Let’s imagine the situation, when we have four forecasting methods applied to 100 time series with accuracy measured in terms of RMSSE:

smallCompetition <- matrix(NA, 100, 4, dimnames=list(NULL, paste0("Method",c(1:4))))
smallCompetition[,1] <- rnorm(100,1,0.35)
smallCompetition[,2] <- rnorm(100,1.2,0.2)
smallCompetition[,3] <- runif(100,0.5,1.5)
smallCompetition[,4] <- rlnorm(100,0,0.3)

We can check the mean and median error measures in this example in order to see, how the methods perform overall:

overalResults <- matrix(c(colMeans(smallCompetition),apply(smallCompetition,2,median)),
                        4, 2, dimnames=list(colnames(smallCompetition),c("Mean","Median")))
round(overalResults,5)

          Mean   Median
Method1 0.99869 1.01157
Method2 1.18413 1.19839
Method3 1.00315 1.00768
Method4 1.08543 1.04730

In this artificial example, it looks like the most accurate method in terms of mean RMSSE is Method 1, and the least accurate one is Method 2. When it comes to medians, then Method 3 is winning. However, the difference in terms of accuracy between methods 1, 3 and 4 does not look big, especially in terms of median measures. So, should we conclude that the Method 1 is the best or should we prefer Method 3? Let's first look at the distribution of errors:

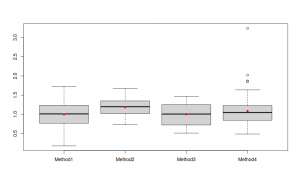
boxplot(smallCompetition)
points(colMeans(smallCompetition),col="red",pch=16)

What these boxplots show is that the distribution of errors for the Method 2 is shifted higher than the distributions of other methods, but it also looks like Method 2 is working more consistently, meaning that the variability of the errors is lower (the size of the box on the graph; sure, it has the lowest sd in the data generation). It's difficult to tell whether Method 1 is better than Method 3 or not - their boxes intersect and roughly look similar, with Method 3 having shorter whiskers and Method 1 having the box slightly lower positioned. Finally, we can see that Method 4 fails in several cases (the outliers on the boxplot).

This is all the basics of descriptive statistics, which allows to conclude that in general Methods 1 and 3 do slightly better job than the Method 2 and probably Method 4 as well. This is also reflected in the mean and median error measures, discussed above. So, what should we conclude? Do we choose Method 1 or Method 3?

Let's not make hasty decisions. Don't forget that we are dealing with a sample of data (100 time series), so inevitably the performance of methods will change if we try them on different data sets. If we had a population of all the time series in the world, then we could run our methods (how much time would it take though?) and make a more solid conclusion about their performance. But here we deal with a sample. So it might make sense to see, whether the difference in performance of methods is significant. How should we do that?

First, we can compare means of distributions of errors using a parametric statistical test. We can try F-test, which will tell us whether the mean performance of methods is similar or not. Unfortunately, this will not tell us, how the methods compare. t-test could be used to do that instead for pairwise comparison. One could also use a regression with dummy variables for methods, which will then give us parameters and their confidence intervals (based on t-statistics), telling us, how the means of methods compare. However F-test, t-test and t-statistics from regression rely on strong assumptions related to the distribution of the means of error measures (normality). If we had large sample (e.g. a thousand of series), then we could try it, hoping that central limit theorem would work, and might get something relatively meaningful. However, on 100 observations this still could be an issue, especially given that the distribution of error measures is typically asymmetric (this means that the estimate of mean might be biased, which leads to a lot of issues).

Second, we could compare medians of distributions of errors. They are robust to outliers, so their estimates should not be too biased in case of skewed distributions on smaller samples. In order to have a general understanding of performance (is everything the same or is there at least one method that performs differently), we could try Friedman test, which could be considered as a non-parametric alternative of F-test. This should work in our case, but won't tell us how specifically the methods compare. We could try Wilcoxon signed-ranks test, which could be considered as a non-parametric counterpart of t-test, but it is only applicable for the comparison of two variables, while we want to compare four.

Luckily, there is Nemenyi test (Demšar, 2006), which is equivalent to MCB test (Koning et al., 2005). What the test does, is it ranks performance of methods for each time series and then takes mean of those ranks and produces confidence bounds for those means. The means of ranks correspond to medians, so this means that by using this test, we compare medians of errors of different methods. If the confidence bounds for different methods intersect, then we can conclude that the medians are not different from statistical point of view. Otherwise, we can see which of the methods has higher rank, and which has the lower one. There are different ways how to present the results of the test, the nemenyi() function from tsutils package implements it and gives several options for plotting (it is discussed in more detail in Nikos' post about the tsutils package). I personally prefer MCB style:

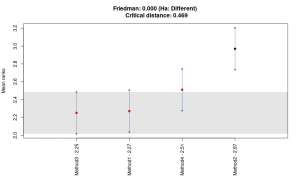
library(tsutils)
nemenyi(smallCompetition, plottype="mcb")

The graph above tells us that methods 1, 3 and 4 have similar medians on 95% confidence level (because their bounds intersect), with Method 3 having the smallest one, then Method 1 and after that - Method 4. This corresponds to the medians discussed above. Finally, Method 2 has the highest median and the difference between it and Methods 1 and 3 is statistically significant on 5% significance level (the confidence bounds do not intersect between Method 2 and Methods 1 / 3). Interestingly enough, bounds of Methods 2 and 4 do intersect, so we cannot tell the difference between them. But we still can conclude that Method 2 is performing poorly, and that the other three methods do not differ significantly. The situation might change if we have a larger sample of time series, where the confidence intervals might become shorter, but it is what it is on our sample.

An alternative to nemenyi(), which should give roughly the same results is using regression with dummy variables on ranks and then using the parameters and their confidence intervals for ranking and determining the significance in difference between the methods. F-test can also be used to determine if the differences are significant overall. The more statistically correct approach to the problem would be using ordinal logistic regression, but given the simplicity of the problem, the linear regression should suffice. Furthermore, it's easier to work with and easier to interpret than the ordinal regression. rmcb() function from greybox package implements this approach (this was already discussed in one of the previous posts about the greybox package). This is a faster method than nemenyi(), especially on big datasets. Here is an example on our data:

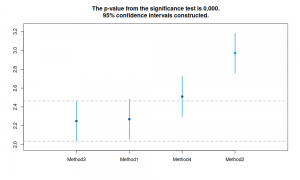
library(greybox)
ourTest <- rmcb(smallCompetition,plottype="none")
ourTest
plot(ourTest,"mcb")

Regression for Multiple Comparison with the Best
The significance level is 5%
The number of observations is 100, the number of methods is 4
Significance test p-value: 0

The result of this test reads similar to nemenyi(): methods 3, 1 and 4 perform similar in terms of median RRMSE and Method 2 is significantly worse than the three. The main difference between the two approaches is in the critical distances: nemenyi() relies on Studentised range distribution, while rmcb() uses Student's T distribution. Both take into account the number of methods, but the critical value for the first one is more sensitive to this than for the second one. So, typically rmcb() will have narrower bounds than nemenyi(), although the difference might be negligible and will disappear with the increase of the sample size. In our example, there is a difference: previously we concluded that the medians of Method 2 and Method 4 are not significantly different on 5%, but rmcb() tells us that they are significantly different. This contradiction should disappear with the increase of the sample size, so I would recommend using rmcb() on larger samples.

As for the conclusions based on the analysis we have carried out, it appears that although the methods perform slightly differently, we cannot tell the difference between some of them (3, 1 and 4). We would need to collect more data in order to reach more adequate conclusions. It might be the case that with the increase of the number of time series, the methods will still perform similar, or it might be the case that the uncertainty in the parameters will decrease and we will see a clear winner. But if you still find that several methods do a similar job, then it might make sense to take some other factors into account, when selecting the best one: for example, which of the methods is simpler or which of them takes less computational time. Still, using statistical tests for the comparison is a good idea, as they might give you a better understanding of what you are dealing with.