I’ve seen several times ML experts applying principles of classification for intermittent demand forecasting. For example, they try predicting, WHEN the demand will happen. This is not a very sensible thing to do.

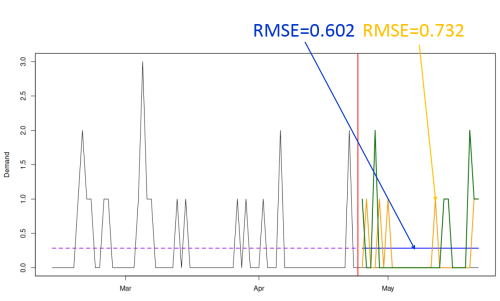
The featured image in this post shows two forecasting approaches: one that tries to predict when demand happens (the yellow line), and the other one that tries capturing the structure of the demand and extrapolates it (the blue line). The green line shows the values in the holdout, and the RMSE indicates the error of the two approaches. Apparently, the straight line is better in this example. Let’s discuss why.

Just a reminder, intermittent demand is the demand that happens at irregular frequency. By definition, we cannot know when a person will come to our store and buy the product. We operate with probabilities in this case, and can say sometimes that the probability of purchase goes up or down due to some factors (seasonality, holidays, promotion etc). When a spherical ML expert in vacuum hears about probability, the first thing that pops to their mind is the “decision boundary” for classification task. Why not set some threshold and say that if the probability is higher than that, the product will be bought and in the other case it won’t?

Well, while this works in classification, it typically doesn’t make sense in demand forecasting.

First, there’s not much structure to capture in intermittent demand besides the basic level, external factors, such as promotions and calendar effects, and occasional trend. Yes, some of them might change the probability of occurrence, and, for example, show that a product will be bought on Monday with 90% probability. This still does not mean that the product will be indeed bought. Saying that it will is just informed guessing, not forecasting.

Second, point forecast is supposed to capture the structure and filter out the noise (see this post). In case of intermittent demand, the structure consists of two parts: expected occurrence (probability) and demand sizes. If we substitute the probability with zeroes and ones based on some threshold, we’ll end up overfitting the noise, but on a different level than usually: the future is uncertain and we can never say for sure what will happen and when, yet we would be playing a guessing game, hoping to be correct. It is like tossing a coin, trying to guess how it will land next time. If you want to have an expectation in that experiment, you should have probability, not a sequence of zeroes and ones.

Third and most important, working with intermittent demand, we typically want to solve a specific problem. The classical example is inventory management, in which case we don’t care whether customers will come and buy our product on Monday, instead of Tuesday. We care about having enough product on shelves to satisfy customers throughout a period of time, while our product is being delivered (lead time). So, the goal in this case is to identify the appropriate safety stock level based on the current stock and thus get an estimate of the demand over lead time, not to predict when people come and how much they will buy. Focusing on the point forecast in this setting is a futile task.

So, when working with intermittent demand, don’t waste your time on trying to forecast when the demand will happen. Focus instead on getting the structure correctly and then understanding what is needed by decision makers and how it will be used.