We continue our discussion of error measures (if you don’t mind). One other thing that you encounter in forecasting experiments is tables containing several error measures (MASE, RMSSE, MAPE, etc.). Have you seen something like this? Well, this does not make sense, and here is why.

The idea of reporting several error measures comes from forecasting competitions, one of the findings of which was that the ranking of methods might differ depending on what error measure you use. But this is so 20th-century thing to do! We are now in the 21st century and have a much better understanding of what to measure and how.

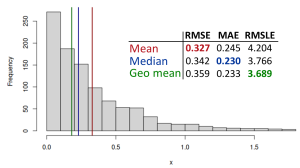
I should start with the maxima very well summarised by Stephan Kolassa (2016 and 2020): MAE-based measures are minimised by the median of a distribution, while the RMSE-based ones are minimised by the mean. To illustrate this point, see the following image of a distribution of a variable x:

What you see in that image is a histogram with three vertical lines: red for mean, blue for median and green for the geometric mean. To the right of the histogram, you can see a small table with the three error measures (read more about them here): RMSE (Root Mean Squared Error), MAE (Mean Absolute Error), and RMSLE (Root Mean Squared Logarithmic Error, based on difference in logarithms). You can see that RMSE is minimised by the mean, MAE is minimised by the median and the RMSLE is minimised by the geometric mean. And this happens by design, not by coincidence.

So what?

Well, this just tells us that it does not make sense to use all three error measures, because they measure different things. If your models produce conditional means (this is what the majority of them do by default), use RMSE-based measure – there is no point in showing how those models also perform in terms of MAPE/MASE, or whatever else. If your model produces conditional mean, fails in terms of RMSE, but does a good job in terms of MAPE, then it is probably not doing a good job overall. It is like saying that my bicycle isn’t great for riding, but it excels at hammering nails. So, think what you want to measure and measure it! And if you want to measure a temperature, don’t use a ruler!

Having said that, I should confess that I used to report several measures in my papers until a few years back. This is because I did not understand this idea very well. But I have realised my mistake, and now I am trying to avoid this and stick to those measures that make sense for the task at hand.

Another story is whether you are interested in the accuracy of point forecasts, their bias or the performance of a model in terms of quantiles. In that case you might need a completely different set of error measures. But I might come back to this in a future post.