18.3 Prediction intervals
A prediction interval is needed to reflect the uncertainty about the data. In theory, the 95% prediction interval will cover the actual values in 95% of the cases if the model is correctly specified. The specific formula for the prediction interval will vary with the assumed distribution. For example, for the Normal distribution (assuming that \(y_{t+j} \sim \mathcal{N}(\mu_{y, t+j}, \sigma_j^2)\)) we will have the classical one: \[\begin{equation} y_{t+j} \in (\hat{y}_{t+j} + z_{\alpha/2} \hat{\sigma}_j, \hat{y}_{t+j} + z_{1-\alpha/2} \hat{\sigma}_j), \tag{18.2} \end{equation}\] where \(\hat{y}_{t+j}\) is the estimate of \(\mu_{y,t+j}\), \(j\) steps ahead conditional expectation, \(\hat{\sigma}_j^2\) is the estimate of \({\sigma}_j^2\), \(j\) steps ahead variance of the error term obtained using principles discussed in Subsection 18.2.3 (for example, calculated via the formula (5.12)), and \(z\) is z-statistics (quantile of Standard Normal distribution) for the selected significance level \(\alpha\).
Remark. Note that \(\alpha\) has nothing to do with the smoothing parameters for the level of ETS model.
This type of prediction interval can be called parametric. It assumes a specific distribution and relies on the other assumptions about the constructed model (such as residuals are i.i.d., see Section 14). Most importantly, it assumes that the \(j\) steps ahead value follows a specific distribution related to the one for the error term. In the case of Normal distribution, the assumption \(\epsilon_t\sim\mathcal{N}(0,\sigma^2)\) implies that \(y_{t+1}\sim\mathcal{N}(\mu_{y,t+1}, \sigma_1^2)\) and due to the convolution of random variables (the sum of random variables follows the same distribution as individual variables, but with different parameters), that \(y_{t+j}\sim\mathcal{N}(\mu_{y,t+j},\sigma_j^2)\) for all \(j\) from 1 to \(h\).
The interval produced via (18.2) corresponds to two quantiles from the Normal distribution and can be written in a more general form as: \[\begin{equation} y_{t+j} \in \left(q \left(\hat{y}_{t+j},\hat{\sigma}_j^2,\frac{\alpha}{2}\right), q\left(\hat{y}_{t+j},\hat{\sigma}_j^2,1-\frac{\alpha}{2}\right)\right), \tag{18.3} \end{equation}\] where \(q(\cdot)\) is a quantile function of an assumed distribution, \(\hat{y}_{t+j}\) acts as a location, and \(\hat{\sigma}^2\) acts as a scale of distribution. Using this general formula (18.3) for prediction intervals, we can construct them for other distributions as long as they support convolution. In the ADAM framework, this works for all pure additive models that have an error term that follows one of the following distributions:
- Normal: \(\epsilon_t \sim \mathcal{N}(0, \sigma^2)\), thus \(y_{t+j} \sim \mathcal{N}(\mu_{y, t+j}, \sigma_j^2)\);
- Laplace: \(\epsilon_t \sim \mathcal{Laplace}(0, s)\) and \(y_{t+j} \sim \mathcal{Laplace}(\mu_{y, t+j}, s_j)\);
- Generalised Normal: \(\epsilon_t \sim \mathcal{GN}(0, s, \beta)\), so that \(y_{t+j} \sim \mathcal{GN}(\mu_{y, t+j}, s_j, \beta)\);
- S: \(\epsilon_t \sim \mathcal{S}(0, s)\), \(y_{t+j} \sim \mathcal{S}(\mu_{y, t+j}, s_j)\).
If a model has multiplicative components or relies on a different distribution, then the several steps ahead actual value will not necessarily follow the assumed distribution, and the formula (18.3) will produce incorrect intervals. For example, if we work with a pure multiplicative ETS model, ETS(M,N,N), assuming that \(\epsilon_t \sim \mathcal{N}(0, \sigma^2)\), the two steps ahead actual value can be expressed in terms of the values on observation \(t\): \[\begin{equation} y_{t+2} = l_{t+1} (1+\epsilon_{t+2}) = l_{t} (1+\alpha \epsilon_{t+1}) (1+\epsilon_{t+2}) , \tag{18.4} \end{equation}\] which introduces the product of Normal distributions, and thus \(y_{t+2}\) does not follow Normal distribution anymore. In such cases, we might have several options of what to use to produce intervals. They are discussed in the subsections below.
18.3.1 Approximate intervals
Even if the actual multistep value does not follow the assumed distribution, we can use approximations in some cases: the produced prediction interval will not be too far from the correct one. The main idea behind the approximate intervals is to rely on the same distribution for \(y_{t+j}\) as for \(y_{t+1}\), even though we know that the variable will not follow it. In the case of multiplicative error models, the limit (6.5) can be used to motivate the usage of that assumption: \[\begin{equation*} \lim\limits_{x \to 0}\log(1+x) = x . \end{equation*}\] For example, in the case of the ETS(M,N,N) model, we know that \(y_{t+2}\) will not follow the Normal distribution, but if the variance of the error term is low (e.g. \(\sigma^2 < 0.05\)) and the smoothing parameter \(\alpha\) is close to zero, then the Normal distribution would be a satisfactory approximation of the real one. This becomes clear if we expand the brackets in (18.4): \[\begin{equation} y_{t+2} = l_{t} (1 + \alpha \epsilon_{t+1} + \epsilon_{t+2} + \alpha \epsilon_{t+1} \epsilon_{t+2}) . \tag{18.5} \end{equation}\] With the conditions discussed above (low \(\alpha\), low variance) the term \(\alpha \epsilon_{t+1} \epsilon_{t+2}\) will be close to zero, thus making the sum of Normal distributions dominant in the formula (18.5). The advantage of this approach is in its speed: you only need to know the scale parameter of the error term and the conditional expectation. The disadvantage of the approach is that it becomes inaccurate with the increase of the parameters’ values and scale of the model. The rule of thumb for when to use this approach: if the smoothing parameters are all below 0.1 (in the case of ARIMA, this is equivalent to MA terms being negative and AR terms being close to zero) or the scale of distribution is below 0.05, the differences between the proper interval and the approximate one should be negligible.
18.3.2 Simulated intervals
This approach relies on the idea discussed in Section 18.1. It is universal and supports any distribution because it only assumes that the error term follows the selected distribution (no need for the actual value to do that as well).
The simulated paths are then produced based on the generated values and the assumed model. After generating \(n\) paths, one can take the desired quantiles to get the bounds of the interval. The main issue of the approach is that it is time-consuming (slower than the approximate intervals) and might be highly inaccurate if the number of iterations \(n\) is low. This approach is used as a default in adam() for the non-additive models.
18.3.3 Semiparametric intervals
The three approaches above assume that the residuals of the applied model are i.i.d. (see discussion in Chapter 14). If this assumption is violated (for example, the residuals are autocorrelated), then the intervals might be miscalibrated (i.e. producing wrong values). In this case, we might need to use different approaches. One of these is the construction of semiparametric prediction intervals (see, for example, Lee and Scholtes, 2014). This approach relies on the in-sample multistep forecast errors discussed in Subsection 14.7.3. After producing \(e_{t+j|t}\) for all in-sample values of \(t\) and for \(j=1,\dots,h\), we can use these errors to calculate the respective \(h\) steps ahead conditional variances \(\sigma_j^2\) for \(j=1,\dots,h\). These values can then be inserted in the formula (18.3) to get the desired prediction interval. The approach works well in the case of pure additive models, as it relies on specific assumed distribution. However, it might have limitations similar to those discussed earlier for the mixed models and the models with positively defined distributions (such as Log-Normal, Gamma, and Inverse Gaussian). It can be considered a semiparametric alternative to the approximate method discussed above.
18.3.4 Nonparametric intervals
When some of the assumptions might be violated, and when we cannot rely on the parametric distributions, we can use the nonparametric approach proposed by Taylor and Bunn (1999). The authors proposed using the multistep forecast errors to construct the following quantile regression model: \[\begin{equation} \hat{e}_{t+j} = a_0 + a_1 j + a_2 j^2, \tag{18.6} \end{equation}\] for each of the bounds of the interval. The motivation behind the polynomial in (18.6) is because, typically, the multistep conditional variance will involve the square of the forecast horizon. The main issue with this approach is that the polynomial function has an extremum, which might appear sometime in the future. For example, the upper bound of the interval would increase until that point and then start declining. To overcome this limitation, I propose using the power function instead: \[\begin{equation} \hat{e}_{t+j} = a_0 j^{a_1} . \tag{18.7} \end{equation}\] This way, the bounds will always change monotonically, and the parameter \(a_1\) will control the speed of expansion of the interval. The model (18.7) is estimated using quantile regression for the upper and the lower bounds separately, as Taylor and Bunn (1999) suggested. This approach does not require any assumptions about the model and works as long as there are enough observations in-sample (so that the matrix of forecast errors contains more rows than columns). The main limitation of this approach is that it relies on quantile regression and thus will have the same issues as, for example, pinball score has (see discussion in Section 2.2): the quantiles are not always uniquely defined. Another limitation is that we assume that the quantiles will follow the model (18.7), which might be violated in real life scenarios.
18.3.5 Empirical intervals
Another alternative to the parametric intervals uses the same matrix of multistep forecast errors, as discussed earlier. The empirical approach is more straightforward than the approaches discussed above and does not rely on any assumptions (it was discussed in Lee and Scholtes, 2014). The idea behind it is just to take quantiles of the forecast errors for each forecast horizon \(j=1,\dots,h\). These quantiles are then added to the point forecast if the error term is additive or are multiplied by it in the case of the multiplicative one. Trapero et al. (2019) show that the empirical prediction intervals perform on average better than the analytical ones. This is because of the potential violation of assumptions in real life. So, in general, I would recommend producing empirical intervals if it was not for the computational difficulties related to the multistep forecast errors. If you have an additive model and believe that the assumptions are satisfied, then the parametric interval will be as accurate but faster. Furthermore, the approach will be unreliable on small samples due to the same problem with the quantiles as discussed earlier.
18.3.6 Complete parametric intervals
So far, all the intervals discussed above relied on an unrealistic assumption that the parameters of the model are known. This is one of the reasons why the intervals produced for ARIMA and ETS are typically narrower than expected (see, for example, results of a tourism competition, Athanasopoulos et al., 2011). But as we discussed in Section 16, there are ways of capturing the uncertainty of estimated parameters of the model and propagating it to the future uncertainty (e.g. to the conditional \(h\) steps ahead variance). As discussed in Section 16.5, the more general approach is to create many in-sample model paths based on randomly generated parameters of the model. This way, we can obtain a variety of states for the final in-sample observation \(T\) and then use those values to construct final prediction intervals. The simplest and most general way of producing intervals, in this case, is using simulations (as discussed earlier in Subsection 18.3.2). The intervals produced via this approach will be wider than the conventional ones, and their width will be proportional to the uncertainty around the parameters. This also means that the intervals might become too wide if the uncertainty is not captured correctly (see discussion in Section 16.5). One of the main limitations of the approach is its computational time: it will be proportional to the number of simulation paths for both refitted models and prediction intervals.
It is also theoretically possible to use other approaches for the intervals construction in the case of complete uncertainty (e.g. “empirical” one for each of the set of parameters of the model), but they would be even more computationally expensive than the approach described above and will have the limitations similar to the discussed above (i.e. non-uniqueness of quantiles, sample size requirements, etc).
18.3.7 Explanatory variables
In all the cases described above, when constructing prediction intervals for the model with explanatory variables, we assume that their values are known in the future. Even if they are not provided by the user and need to be forecasted, the produced conditional expectations of variables will be used for all the calculations. This is not an entirely correct approach, as was shown in Subsection 10.2.2, but it speeds up the calculation process and typically produces adequate results.
The more theoretically correct approach is to take the multistep variance of explanatory variables into account. This would work for pure additive models for explanatory and response variables but imply more complicated formulae for other models. This is one of the directions of future research.
18.3.8 Example in R
All the types of intervals discussed in this section are implemented for the adam() models in the smooth package. In order to demonstrate how they work and how they differ, we consider an example with an ETS model on BJSales data:
## [1] "AAdN"The model selected above is ETS(A,Ad,N). In order to make sure that the parametric intervals are suitable, we can do model diagnostics (see Chapter 14), producing plots shown in Figure 18.3.
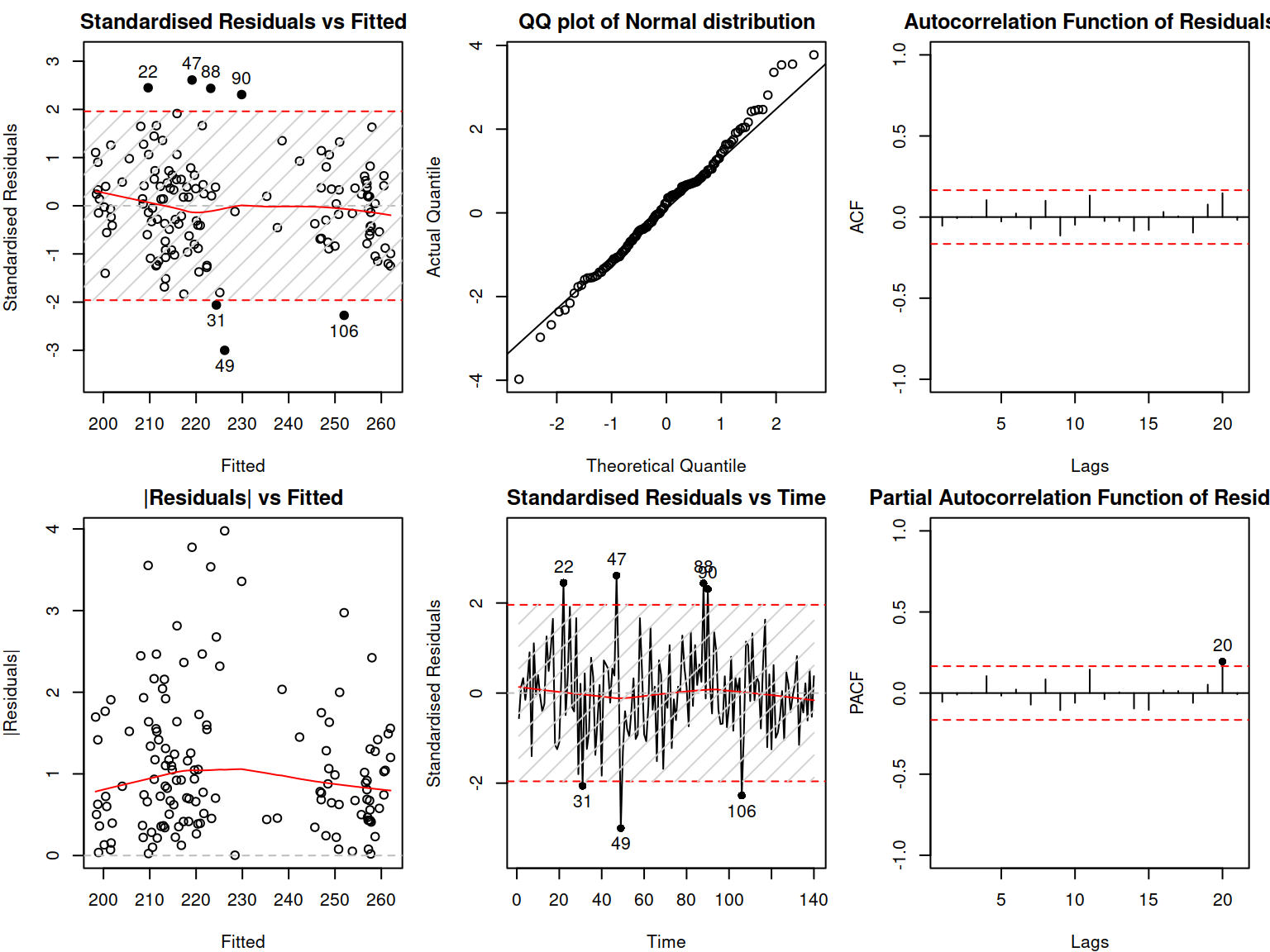
Figure 18.3: Diagnostics of the ADAM on BJSales data.
The model’s residuals do not exhibit any serious issues. Given that this is a pure additive model, we can conclude that the parametric interval would be appropriate for this situation.
The only thing that this type of interval does not take into account is the uncertainty about the parameters, so we can construct the complete interval either via the reforecast() function or using the same forecast(), but with the option interval="complete". Note that this is a computationally expensive operation (both in terms of time and memory), so the more iterations you set up, the longer it will take and the more memory it will consume. The two types of intervals are shown next to each other in Figure 18.4:
par(mfcol=c(1,2), mar=c(2,4,2,1))
forecast(adamETSBJ, h=10, interval="parametric") |>
plot(main="Parametric prediction interval", ylim=c(200,280))
forecast(adamETSBJ, h=10, interval="complete", nsim=100) |>
plot(main="Complete prediction interval", ylim=c(200,280))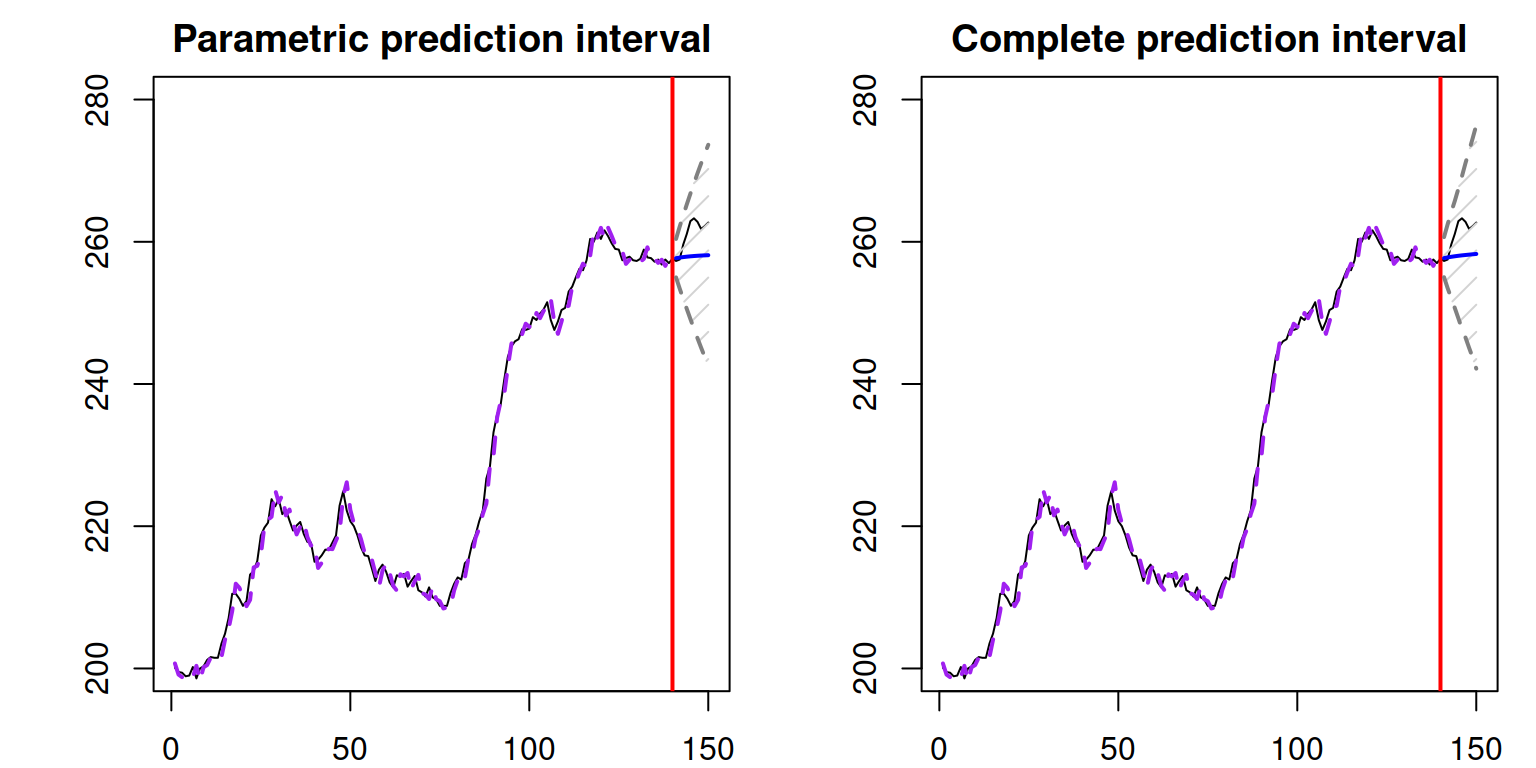
Figure 18.4: Prediction intervals for ADAM on BJSales data.
The resulting complete parametric interval shown in Figure 18.4 is slightly wider than the conventional one. To understand what impacts the complete interval, we can analyse the summary of the model:
##
## Model estimated using adam() function: ETS(AAdN)
## Response variable: BJsales
## Distribution used in the estimation: Normal
## Loss function type: likelihood; Loss function value: 240.2383
## Coefficients:
## Estimate Std. Error Lower 2.5% Upper 97.5%
## alpha 0.9400 0.1093 0.7239 1.0000 *
## beta 0.2998 0.1093 0.0837 0.5157 *
## phi 0.8780 0.0721 0.7354 1.0000 *
##
## Error standard deviation: 1.3655
## Sample size: 140
## Number of estimated parameters: 4
## Number of degrees of freedom: 136
## Information criteria:
## AIC AICc BIC BICc
## 488.4765 488.7728 500.2431 500.9752The smoothing parameters of the model are high, thus the model forgets the initial states fast, and the uncertainty of initial states does not propagate to the last observation as much as in the case of lower values of parameters. As a result, only the uncertainty of smoothing parameters will impact the width of the interval.
Figure 18.5 demonstrates what happens with the fitted values when we take the uncertainty into account.
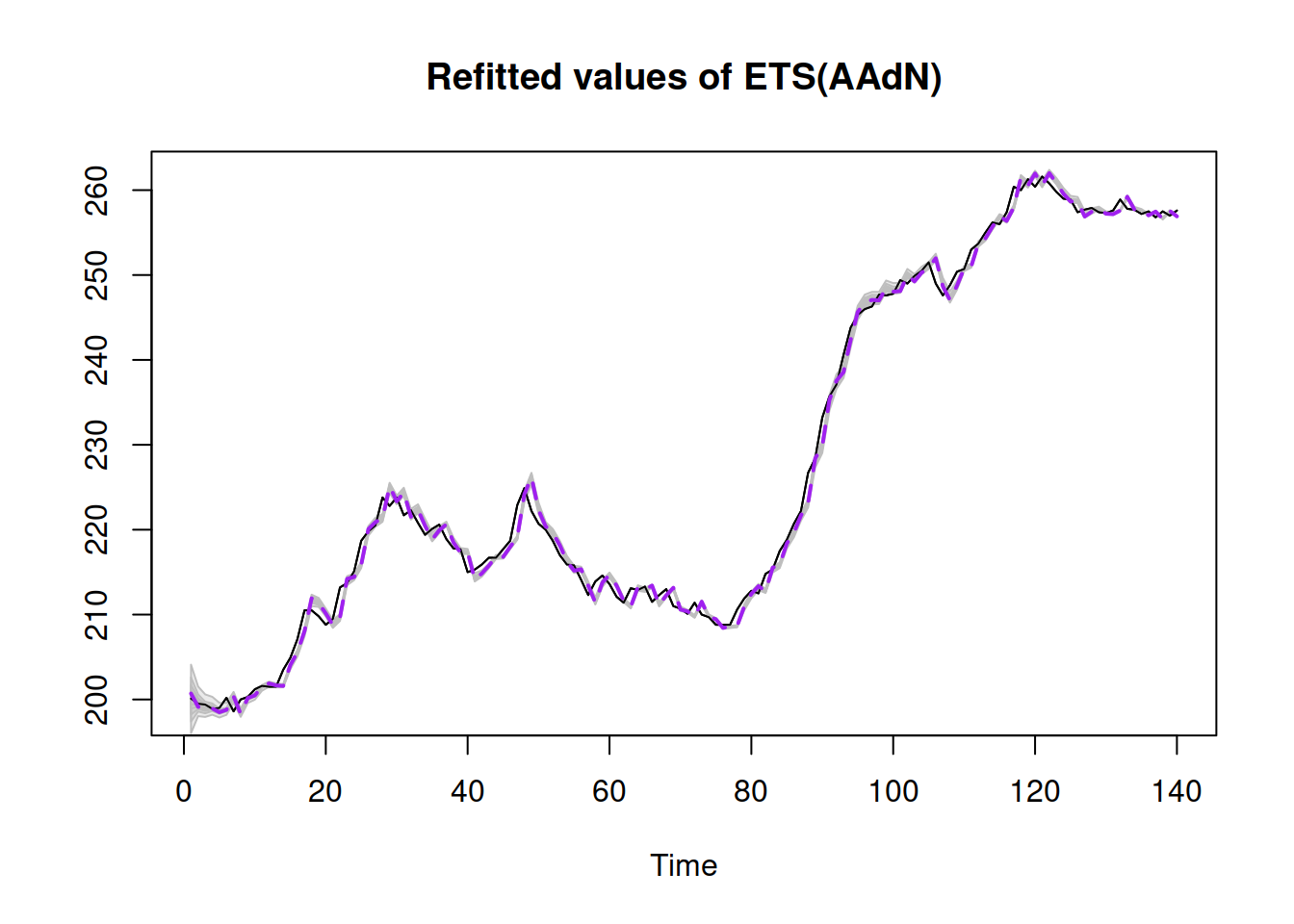
Figure 18.5: Refitted values for ADAM on BJSales data.
As we see from Figure 18.5, the uncertainty around the line is narrow at the end of the sample, so the impact of the initial uncertainty on the forecast deteriorates.
To make things more complicated and exciting, we introduce explanatory variable with lags and leads of the indicator BJsales.lead, automatically selecting the model and explanatory variables using information criteria (see discussion in Chapter 15).
# Form a matrix with response and the explanatory variables
BJsalesData <- cbind(as.data.frame(BJsales),
xregExpander(BJsales.lead,c(-3:3)))
colnames(BJsalesData)[1] <- "y"
# Seletct an ETSX model
adamETSXBJ <- adam(BJsalesData, "YYY",
h=10, holdout=TRUE,
regressors="select")In the code above, I have asked the function specifically to do the selection between pure multiplicative models (see Section 15.1). We will then construct several types of prediction intervals and compare them:
intervalType <- c("approximate", "semiparametric",
"nonparametric", "simulated",
"empirical", "complete")
vector("list", length(intervalType)) |>
setNames(intervalType) -> adamETSXBJPI
for(i in intervalType){
adamETSXBJPI[[i]] <- forecast(adamETSXBJ, h=10,
interval=i)
}These can be plotted in Figure 18.6.
par(mfcol=c(3,2), mar=c(2,2,2,1))
for(i in 1:6){
plot(adamETSXBJPI[[i]],
main=paste0(intervalType[i]," interval"))
}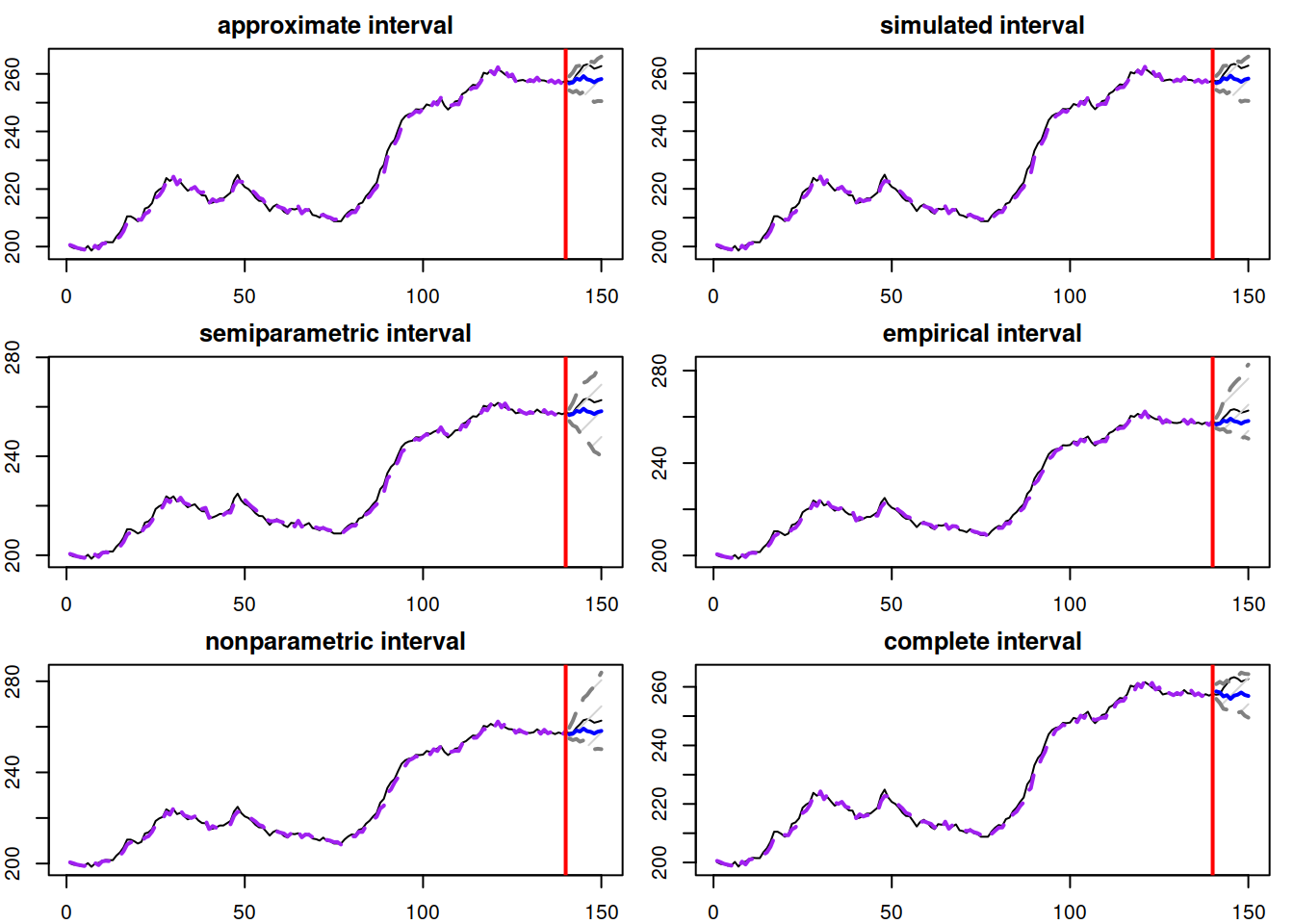
Figure 18.6: Different prediction intervals for ADAM ETS(M,N,N) on BJSales data.
The thing to notice is how the width and shape of intervals change depending on the approach. The approximate and simulated intervals look very similar because the selected model is ETSX(M,N,N) with a standard error of 0.005 (thus, the approximation works well). The complete interval is similar because the estimated smoothing parameter \(\alpha\) equals to one (hence, the forgetting happens instantaneously). However, it has a slightly different shape because the number of iterations for the interval was low (nsim=100 for interval="complete" by default). The semiparametric interval is the widest as it calculates the forecast errors directly but still uses the normal approximation. Both nonparametric and empirical are skewed because the in-sample forecast errors followed skewed distributions, which can be seen via the plot in Figure 18.7:
adamETSXBJForecastErrors <- rmultistep(adamETSXBJ,h=10)
boxplot(1+adamETSXBJForecastErrors)
abline(h=1,col="red")
points(apply(1+adamETSXBJForecastErrors,2,mean),
col="red",pch=16)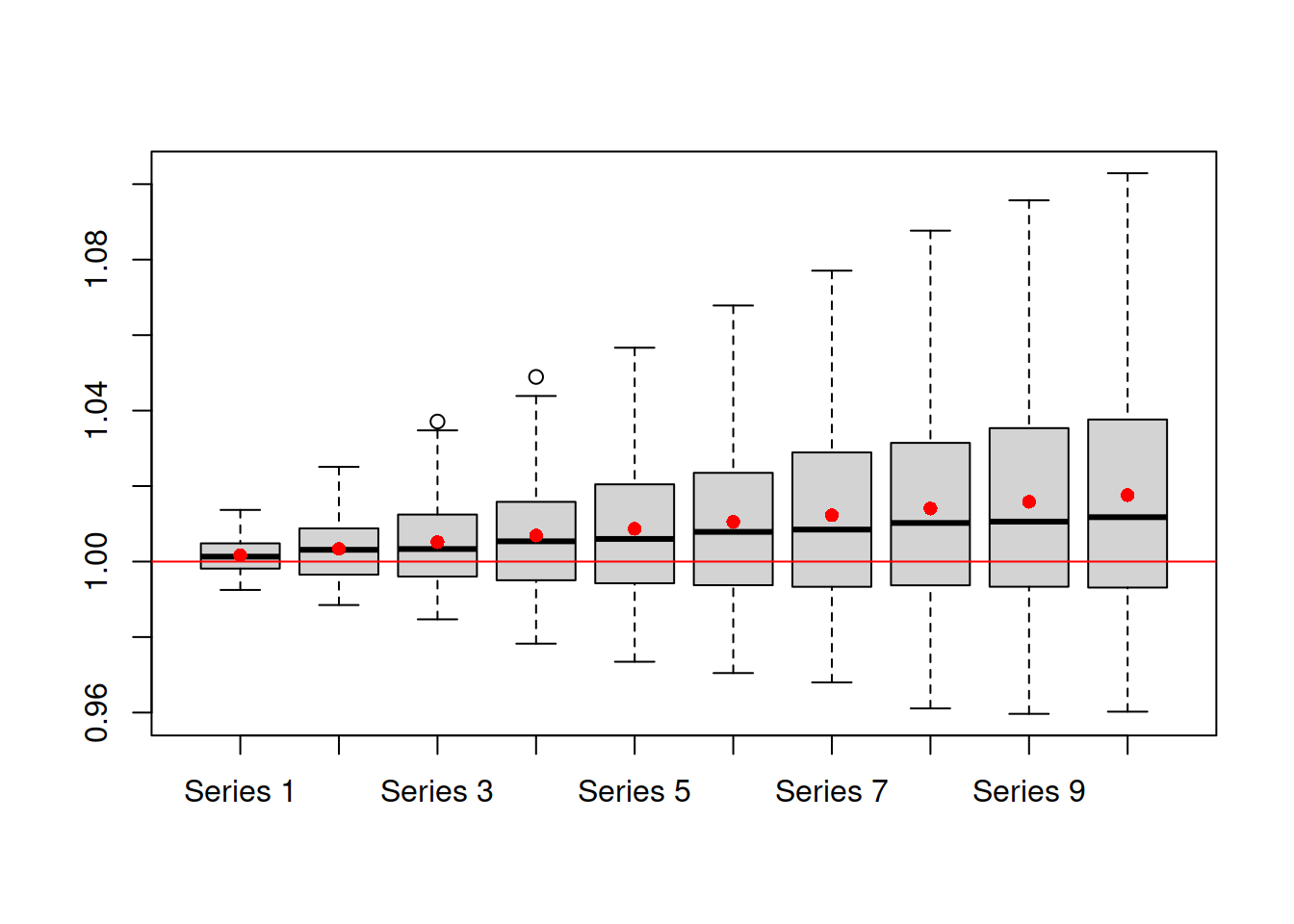
Figure 18.7: Distribution of in-sample multistep forecast errors from ADAM ETSX(M,N,N) model on BJSales data. Red point correspond to mean values.
Analysing the plots in Figure 18.6, it might be challenging to select the most appropriate type of prediction interval. But the model diagnostics (Section 14) might help in this situation:
- If the residuals look i.i.d. and the model does not omit important variables, then choose between parametric, approximate, simulated, and complete interval types:
- “parametric” in case of the pure additive model,
- “approximate” in other cases, when the standard error is lower than 0.05 or smoothing parameters are close to zero,
- “simulated” if you deal with a non-additive model with high values of standard error and smoothing parameters,
- “complete parametric” when the smoothing parameters of the model are close to zero, and you want to take the uncertainty about the parameters into account;
- If residuals seem to follow the assumed distribution but are not i.i.d., then the semiparametric approach might help. Note that this only works on samples of \(T>>h\);
- If residuals do not follow the assumed distribution, but your sample is still larger than the forecast horizon, then use either empirical or nonparametric intervals.
Remark. forecast.adam() will automatically select between “parametric”, “approximate”, and “simulated” if you ask for interval="prediction".
Finally, the discussion from this section also widely applies to ADAM ARIMA and/or Regression. The main difference is that ARIMA/Regression do not have mixed components (as ETS does), so the “parametric” prediction interval can be considered as a standard working option for the majority of cases. The only situation where simulations might be needed is when Log-ARIMA is constructed with Inverse Gaussian or Gamma distributions, because logarithms of these distributions do not support convolutions.