13.4 Examples of application
We consider the same example from Section 13.1. Just as a reminder, in that example, both demand occurrence and demand sizes increase over time (Figure 13.1), meaning that we can try the model with the trend for both parts. This can be done using the adam() function from the smooth package, defining the type of occurrence to use. We will try several options and select the one that has the lowest AICc:
adamiETSy <- vector("list",4)
adamiETSy[[1]] <- adam(y, "MMdN", h=10, holdout=TRUE,
occurrence="odds-ratio")
adamiETSy[[2]] <- adam(y, "MMdN", h=10, holdout=TRUE,
occurrence="inverse-odds-ratio")
adamiETSy[[3]] <- adam(y, "MMdN", h=10, holdout=TRUE,
occurrence="direct")
adamiETSy[[4]] <- adam(y, "MMdN", h=10, holdout=TRUE,
occurrence="general")
adamiETSyAICcs <-
setNames(sapply(adamiETSy,AICc),
c("odds-ratio", "inverse-odds-ratio",
"direct", "general"))
adamiETSyAICcs## odds-ratio inverse-odds-ratio direct general
## 372.3177 401.4045 368.3242 386.2486Based on this, we can see that the model with direct probability has the lowest AICc. We can show how the model approximates the data and produces forecasts for the holdout:
i <- which.min(adamiETSyAICcs)
par(mfcol=c(2,1), mar=c(2,1,2,1))
plot(adamiETSy[[i]],7)
plot(adamiETSy[[i]]$occurrence,7)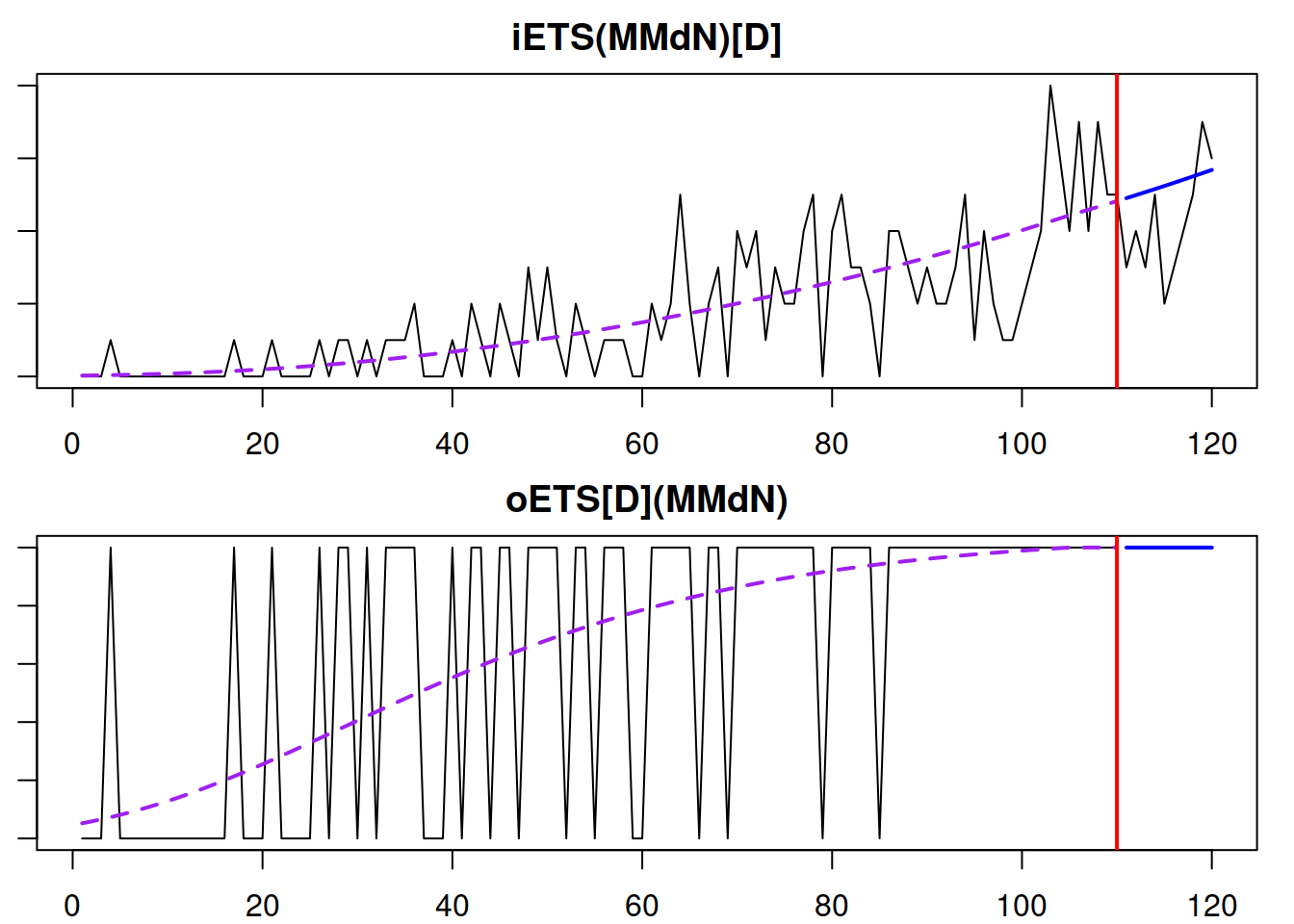
Figure 13.9: The fit of the best model to the intermittent data: final demand and the demand occurrence parts.
Figure 13.9 shows that the model captured the trend well for both the demand occurrence and demand sizes parts. It forecasts that the mean demand will increase for the holdout period. We can also explore the demand occurrence part of this model by typing:
## Occurrence state space model estimated: Direct probability
## Underlying ETS model: oETS[D](MMdN)
## Smoothing parameters:
## level trend
## 0 0
## Vector of initials:
## level trend
## 0.0669 1.1017
##
## Error standard deviation: 1.2373
## Sample size: 110
## Number of estimated parameters: 5
## Number of degrees of freedom: 105
## Information criteria:
## AIC AICc BIC BICc
## 103.3515 103.9284 116.8539 118.2098In our example, the smoothing parameters are equal to zero for the demand occurrence part, which makes sense because the selected model is the damped multiplicative trend one, which should capture the increasing probability of occurrence well.
Depending on the generated data, there might be issues in the ETS(M,Md,N) model for demand sizes, if the smoothing parameters are too big, especially for the trend component. So, we can also try out the logARIMA(1,1,2) to see how it compares with this model. Given that ARIMA is not yet implemented for the occurrence part of the model, we need to construct the oETS separately and then use in adam():
oETSModel <- oes(y, "MMdN", h=10, holdout=TRUE,
occurrence=names(adamiETSyAICcs)[i])
adamiARIMA <- adam(y, "NNN", h=10, holdout=TRUE,
occurrence=oETSModel,
orders=c(1,1,2),
distribution="dlnorm")
adamiARIMA## Time elapsed: 0.08 seconds
## Model estimated using adam() function: iARIMA(1,1,2)[D]
## With optimal initialisation
## Occurrence model type: Direct
## Distribution assumed in the model: Mixture of Bernoulli and Log-Normal
## Loss function type: likelihood; Loss function value: 128.0494
## ARMA parameters of the model:
## Lag 1
## AR(1) -0.2056
## Lag 1
## MA(1) -0.5006
## MA(2) 0.0302
##
## Sample size: 110
## Number of estimated parameters: 6
## Number of degrees of freedom: 104
## Information criteria:
## AIC AICc BIC BICc
## 361.4503 362.2659 377.6532 379.5699
##
## Forecast errors:
## Asymmetry: -70.389%; sMSE: 46.283%; rRMSE: 1.071; sPIS: 3196.776%; sCE: -386.272%Comparing the iARIMA model with the previous iETS based on AICc would not be fair because as soon as the occurrence model is provided to the adam(), it does not count the parameters estimated in that part towards the overall number of estimated parameters. To make the comparison fair, we need to make ADAM iETS comparable by estimating it in a similar way:
## Time elapsed: 0.04 seconds
## Model estimated using adam() function: iETS(MMdN)[D]
## With optimal initialisation
## Occurrence model type: Direct
## Distribution assumed in the model: Mixture of Bernoulli and Gamma
## Loss function type: likelihood; Loss function value: 126.0786
## Persistence vector g:
## alpha beta
## 0.2580 0.0081
## Damping parameter: 1
## Sample size: 110
## Number of estimated parameters: 6
## Number of degrees of freedom: 104
## Information criteria:
## AIC AICc BIC BICc
## 357.5087 358.3242 373.7116 375.6283
##
## Forecast errors:
## Asymmetry: -100%; sMSE: 109.729%; rRMSE: 1.649; sPIS: 5653.118%; sCE: -951.453%Comparing information criteria, the iETS model is more appropriate for this data. But this might be due to different distributional assumptions and difficulties estimating the ARIMA model. If you want to experiment more with iARIMA, you might try fine tuning its parameters (see Section 11.4.1) for the data either by increasing the maxeval or changing the initialisation, for example:
adamiARIMA <- adam(y, "NNN", h=10, holdout=TRUE,
occurrence=oETSModel, orders=c(1,1,2),
distribution="dgamma", initial="back")Finally, we can produce point and interval forecasts from either of the models via the forecast() method. Here is an example:
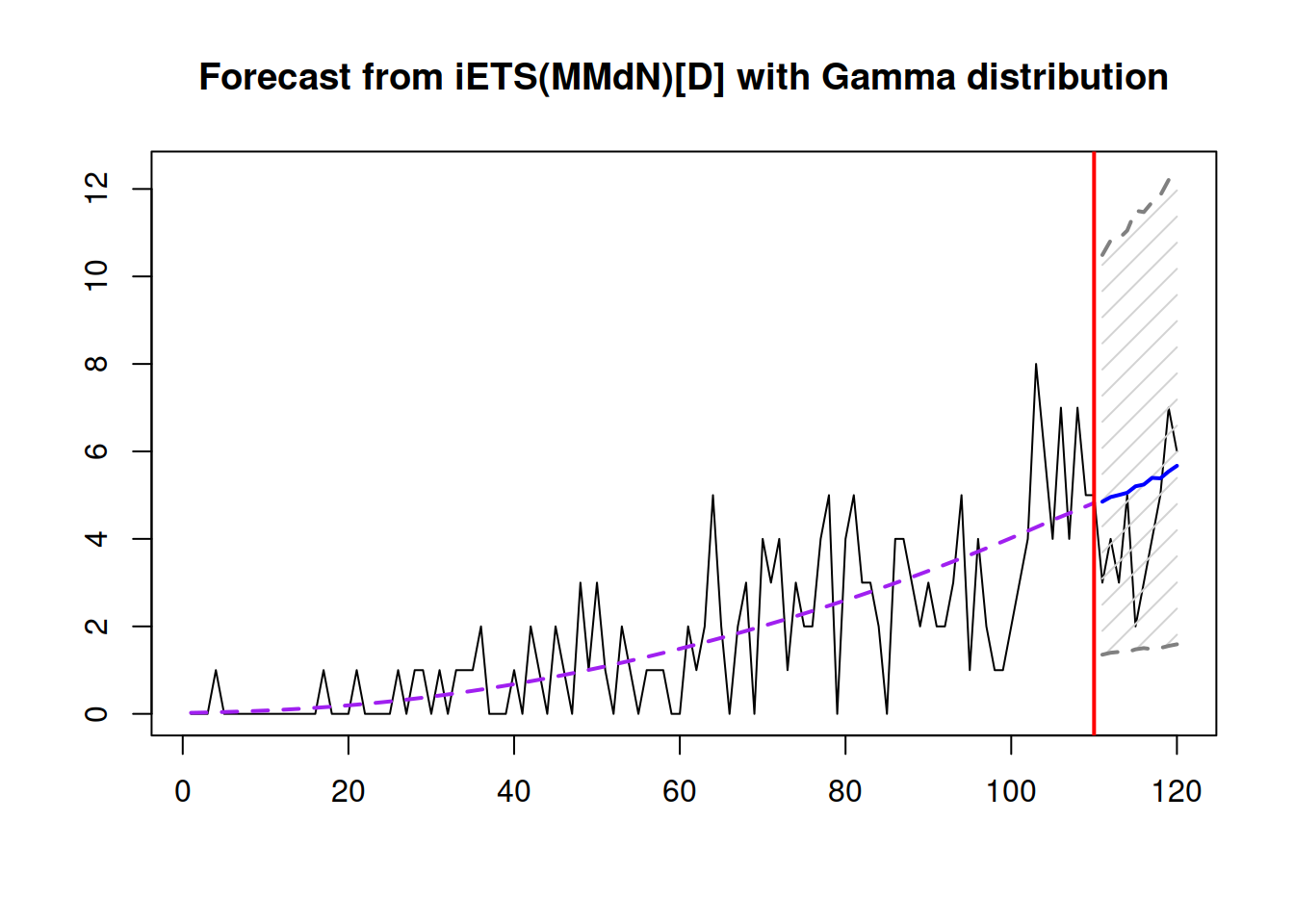
Figure 13.10: Point forecasts and prediction interval from the iETS(M,Md,N)\(_D\) model.
In Figure 13.10, the interval is expanding, reflecting the captured tendency of growth in the data. The prediction interval produced from multiplicative ETS models will typically be simulated if interval="prediction", so to make them smoother, you might need to increase the nsim parameter, for example, to nsim=100000.