14.2 Model specification: Redundant variables
While there are some ways of testing for omitted variables, the redundant ones are sometimes even more challenging to diagnose. Yes, we could look at the significance of variables (Section 7.1 of Svetunkov and Yusupova, 2025) or compare models with and without some variables based on information criteria (Section 16.4 of Svetunkov and Yusupova, 2025): this will show which variables contribute towards the model fit, and which do not. However, even if our approaches say that a variable is not significant, this does not mean that it is not needed in the model. There can be many reasons why a test would fail to reject H\(_0\): \(a_j=0\), and AIC would prefer a model without the variable under consideration. So, in the end, it comes to using judgment, trying to figure out whether a variable is needed in the model or not.
In the example with Seatbelt data, DriversKilled would be a redundant variable for the reasons explained in Section 14.1. Let us see what happens with the model if we include it:
adamSeat04 <- adam(Seatbelts, "NNN",
formula=drivers~PetrolPrice+kms+
law+DriversKilled)
par(mfcol=c(2,1), mar=c(4,4,2,1))
plot(adamSeat04,7:8)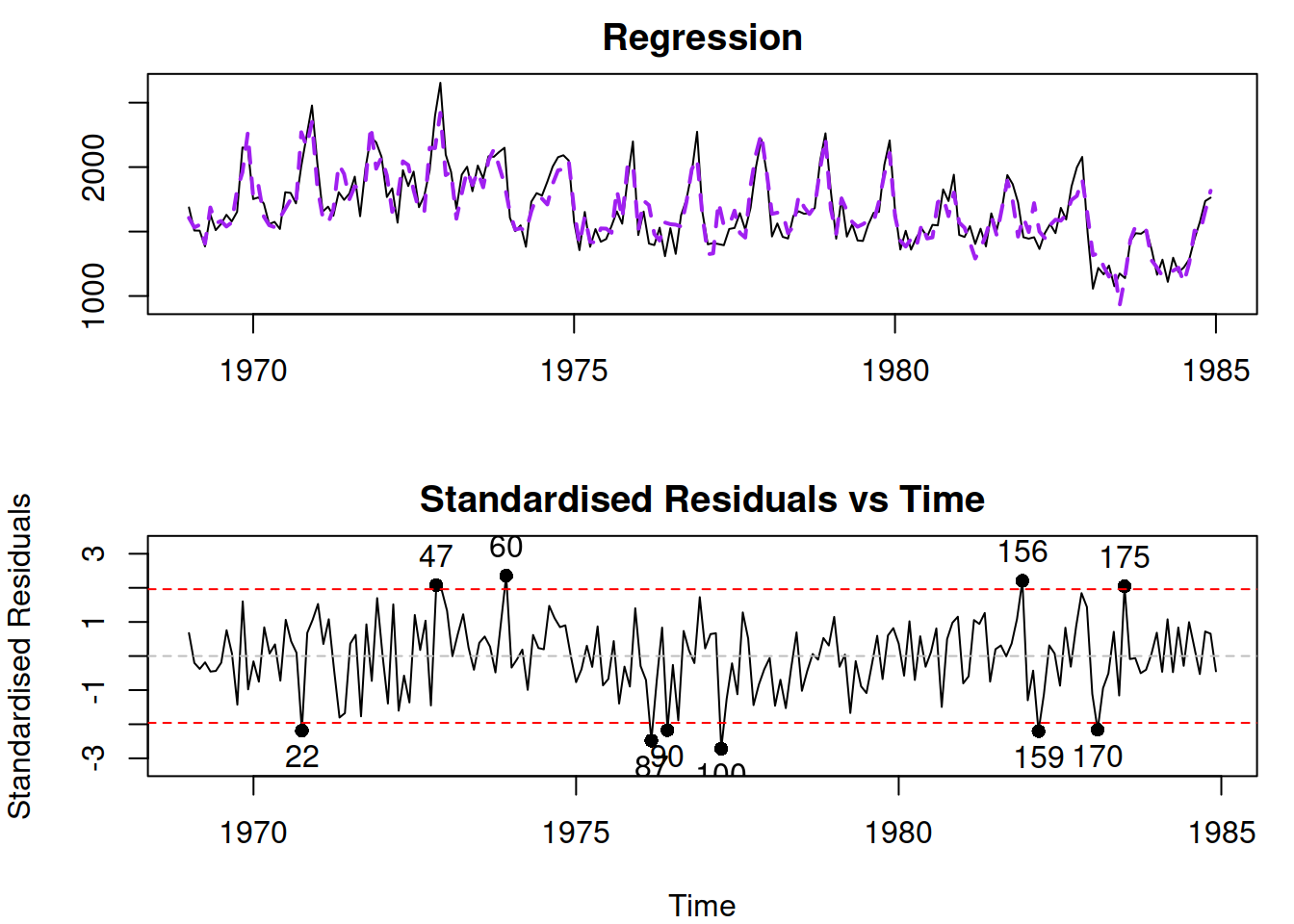
Figure 14.6: Diagnostic plots for Model 4.
The residuals from this model look adequate, and it is not apparent that there is an issue in the model. The summary of this model is:
##
## Model estimated using alm() function: Regression
## Response variable: drivers
## Distribution used in the estimation: Normal
## Loss function type: likelihood; Loss function value: 1189.274
## Coefficients:
## Estimate Std. Error Lower 2.5% Upper 97.5%
## (Intercept) 905.6559 115.0935 678.6073 1132.6294 *
## PetrolPrice -1603.7772 827.8145 -3236.8326 28.7384
## kms -0.0112 0.0035 -0.0182 -0.0043 *
## law -91.2672 31.9765 -154.3483 -28.2070 *
## DriversKilled 9.0423 0.3831 8.2866 9.7978 *
##
## Error standard deviation: 120.1081
## Sample size: 192
## Number of estimated parameters: 5
## Number of degrees of freedom: 187
## Information criteria:
## AIC AICc BIC BICc
## 2388.549 2388.871 2404.836 2405.684The uncertainty around the parameter DriversKilled is narrow, showing that the variable positively impacts the drivers. If we used automated techniques for variables selection (based on AIC or statistical tests), we would conclude that the variable is important and is needed in the model. However, the issue here is not statistical but rather fundamental: we have included the variable that is a part of our response variable. It does not explain why drivers get injured and killed, it just reflects a part of the variable itself. So it approximates some proportion of the variance, which should have been explained by other variables (e.g. PetrolPrice), making them statistically not significant. So, based on the technical analysis, we would be inclined to keep the variable, but based on our understanding of the problem, we should not.
When it comes to the impact of this issue on forecasting, if the model contains redundant variables then it will overfit the data, which could lead to narrower prediction intervals and biased point forecasts. The parameters of such models are typically unbiased but inefficient (Section 6.3 of Svetunkov and Yusupova, 2025).