Chapter 13 Regression with categorical variables
So far we assumed that the explanatory variables in the model are numerical (e.g. length of a tree or years of experience). But is it possible somehow to capture the effect of categorical variables on the variable of interest? Do we expect, for example, sales of silver mobile phone to differ from the sales of the pink one? We probably do, and this needs to be taken into account by a model.
Consider the same example with the overall costs of construction from Chapter 11. The type of building there is a categorical variable, which takes values:
- Detached;
- Semi-detached;
- Other.
If we analyse the spread plot diagram for the original dataset, we will notice that the overall costs seem to change depending on the property type (Figure 13.1):
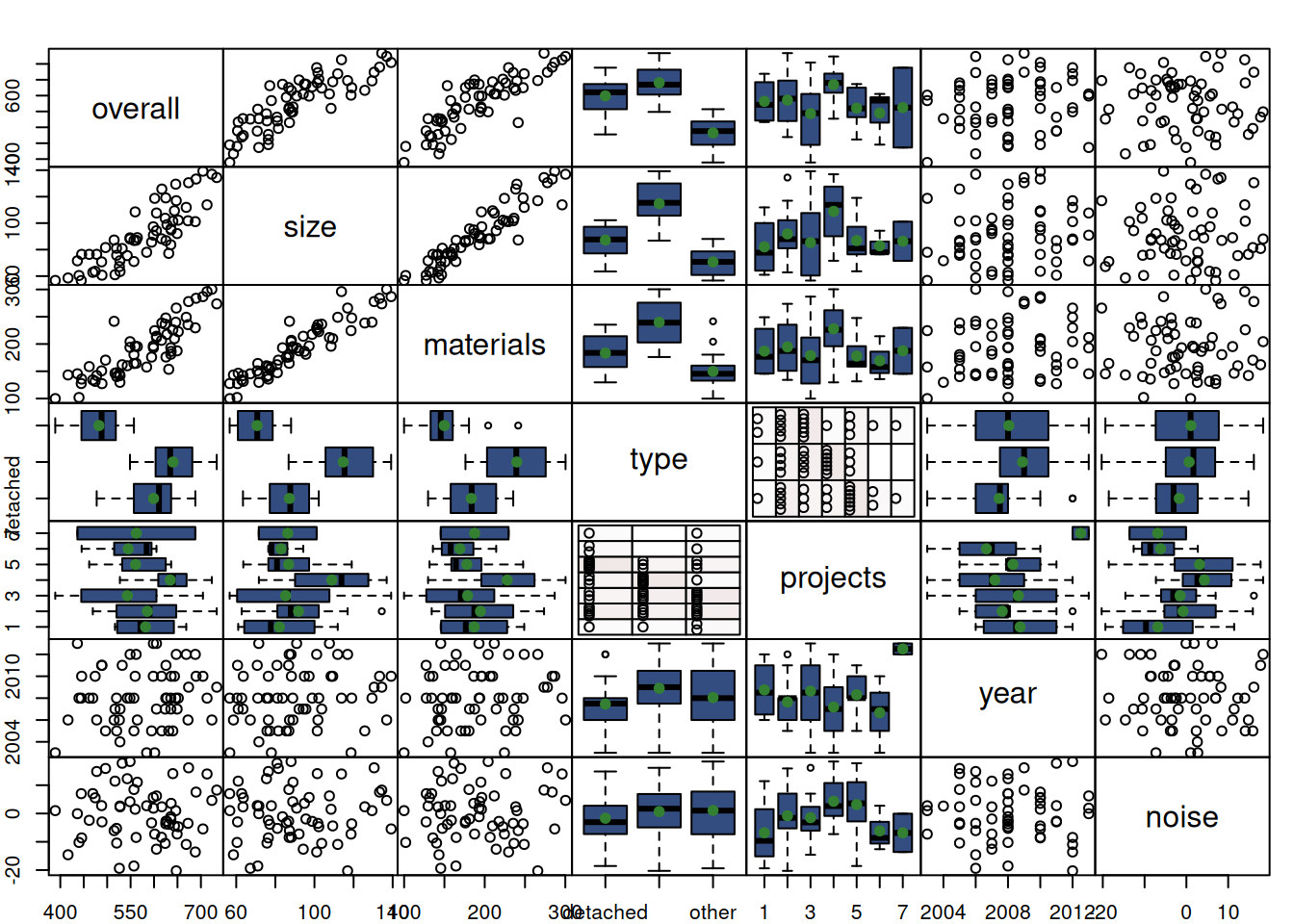
Figure 13.1: Spread plots of the variables in the dataset.
In fact, judging by the boxplots in Figure 13.1, we can see that material costs, sizes of properties and overall costs differ depending on the type of the property. So, this categorical variable has an affect on the project and needs to be taken into account.
If we had a sample large enough, we could split it into three sub-samples depending on the value of the variable and estimate three regression models. Unfortunately, this is neither always possible nor meaningful. If we fit three different models to the data, that would imply that the effect of size, materials costs, number of projects and year when the project started would differ depending on the type of the building. While this might hold for some relations, it is not universally the case. Besides, having three smaller samples instead of one big one, would imply the increased uncertainty about the estimates of parameters of a model (discussed in Chapter 12), thus impacting the managerial decisions based on our model. So, is there a better way?
The answer to this, is “yes”. This can be done by transforming variables from the categorical scale to the set of binary variables (i.e. taking values of zero or one). These binary variables are called “dummy variables” in the regression context. They denote when a specific attribute is met in the sample.
In this chapter we will learn how this information can be incorporated in a regression model and can be used for analysis and for forecasting.