2.3 The Addition Law: Calculating “OR” Probability
Consider an example of a standard 52-card deck. Suppose we want to answer the question: “What is the probability of picking a card that is a face card (Jack, Queen, King) OR a spade (♠)?”
We can solve this in four clear steps:
- Calculate \(P(F)\): First, we calculate the probability of picking a face card. There are 3 face cards in each of the 4 suits, giving a total of 12 face cards. \(P(F) = \frac{12}{52}\)
- Calculate \(P(S)\): Next, we calculate the probability of picking a spade. There are 13 spades in the deck. \(P(S) = \frac{13}{52}\) A common mistake is to simply add these two probabilities together. However, this would lead to an error because some cards satisfy both conditions and would be counted twice.
- Identify the intersection \(P(F \text{ AND } S)\): We must identify the cards that are both a face card and a spade. These are the Jack of Spades (J♠), the Queen of Spades (Q♠), and the King of Spades (K♠). There are 3 such cards. The probability of this intersection is: \(P(F \text{ AND } S) = \frac{3}{52}\)
- Calculate the final probability \(P(F \text{ OR } S)\): To find the correct probability, we add the individual probabilities and then subtract the intersection to correct for the double-counting. \(P(F \text{ OR } S) = \frac{12}{52} + \frac{13}{52} - \frac{3}{52} = \frac{22}{52}\). Simplifying this fraction gives us our final answer: \(\frac{11}{26}\).
Remark. The “AND” and “OR” operators in mathematics, are typically denote by symbols of intersection and union respectively: \(P(F \text{ AND } S) = P(F \cap S)\), \(P(F \text{ OR } S) = P(F \cup S)\).
2.3.1 The General Addition Law
The Addition Law is our primary tool for calculating the probability of at least one of two or more events occurring. We use it when we are interested in the likelihood of outcome A or outcome B happening. This principle is of immense strategic importance in business scenarios where multiple successful outcomes are possible. For example, in risk assessment, it helps calculate the probability of a project being delayed by any one of several potential factors. As an analyst, you will constantly be asked to evaluate scenarios with multiple paths to success; mastering the Addition Law is your first step towards providing a statistically sound answer.
The process we followed in the card example leads us to the formal rule. The General Addition Law for Probabilities is stated as: \[\begin{equation} P(A \cup B) = P(A) + P(B) - P(A \cap B) \tag{2.3} \end{equation}\]
This concept is easily visualised using a Venn diagram shown in Figure 2.1.
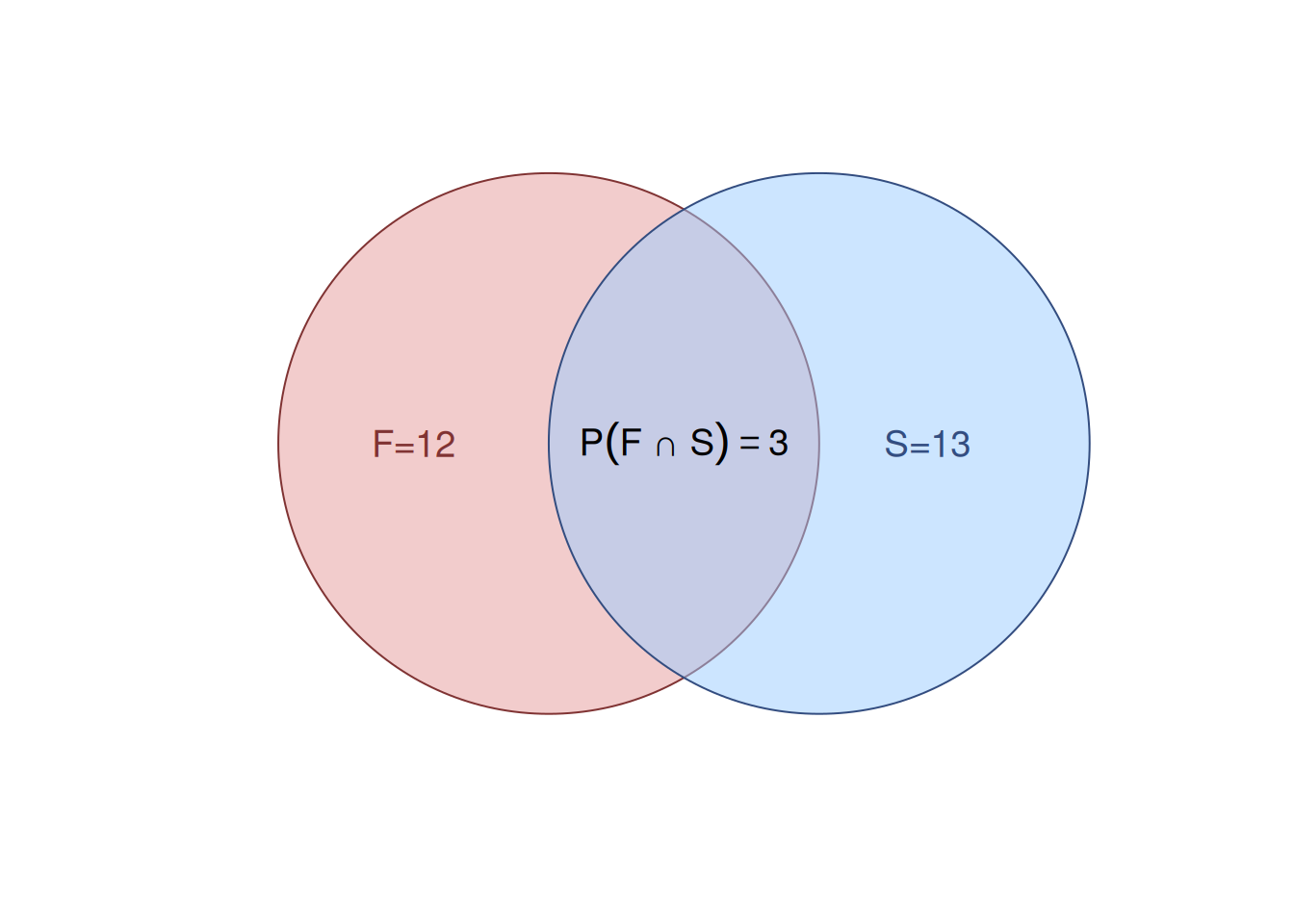
Figure 2.1: Venn diagram for the cards example.
Remark. The union (\(F \cup S\)) in Figure 2.1 corresponds to the overall area of the two circles, while the intersection (\(F \cap S\)) corresponds to the common area between the two circles.
Figure 2.1 shows the number of Face cards (12) in the red area, Spades cards (13) in the blue area, and their intersection in the purple area between them. The overlapping area, \((F \cap S)\), represents those three specific cards that are both face and spades. The formula’s subtraction term, - \(P(A \cap B)\), is simply the mathematical step we take to remove that single layer of double-counting.
2.3.2 Special Case: Mutually Exclusive Events
There is a simpler version of the Addition Law that applies to a special category of events. Mutually exclusive events are events that cannot both happen at the same time; their intersection is zero.
Consider this question: “What is the probability of picking either a Jack or a Queen (of any suit)?”
These two events are mutually exclusive because a single card cannot be both a Jack and a Queen at the same time. This situation can be shown in the Venn diagram in Figure 2.2.
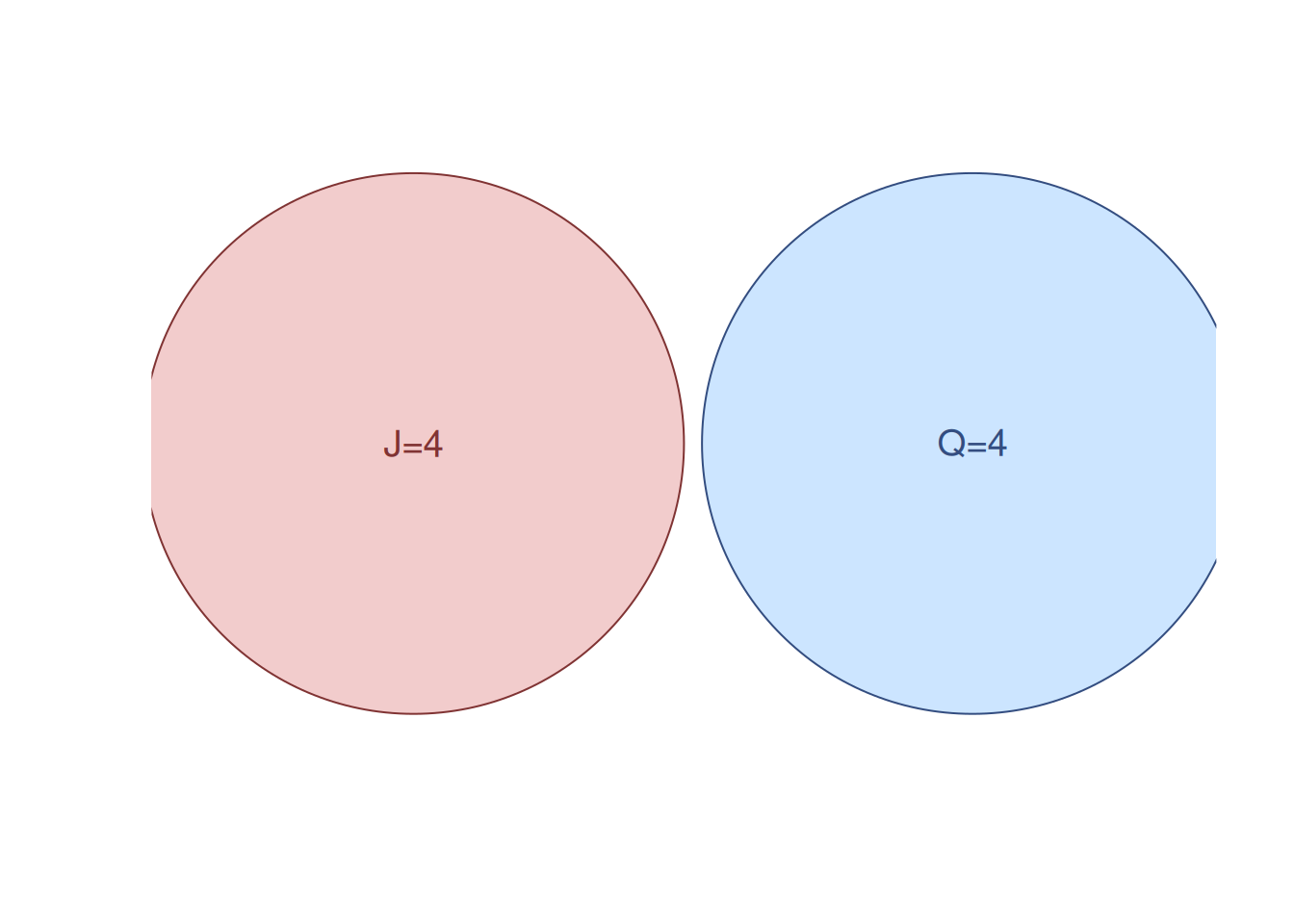
Figure 2.2: Venn diagram for the cards example with mutually exclusive events.
Since there is no overlap, the intersection term \(P(A \cap B)\) is zero. The calculation is therefore a simple sum: \[\begin{equation*} P(J \cup Q) = P(J) + P(Q) = \frac{4}{52} + \frac{4}{52} = \frac{8}{52} = \frac{2}{13}. \end{equation*}\]
This leads to the Addition Law for Mutually Exclusive Events: \[\begin{equation} P(A \cup B) = P(A) + P(B). \tag{2.4} \end{equation}\]